









































I use rpp as an STL replacement, and I’m currently developing a real-time path tracer with it. rpp attempts to provide the following features, roughly in priority order:
Fast Compilation
Including rpp should not increase compilation time by more than 250ms. It must not pull in any STL or system headers—they’re what’s really slow, not templates.
Debugging
User code should be easy to debug. That requires good debug-build performance, defensive assertions, and prohibiting exceptions/RTTI. Concepts should be used to produce straightforward compilation errors.
Performance
User code should have control over allocations, parallelism, and data layout. This is enabled by a region-based allocator system, a coroutine scheduler, and better default data structure implementations. Additionally, tracing-based profiling and allocation tracking are tightly integrated.
Explicitness
All non-trivial operations should be visible in the source code. That means prohibiting implicit conversions, copies, and allocations, as well as using types with clear ownership semantics.
Metaprogramming
It should be easy to perform compile-time computations and reflect on types. This involves pervasive use of concepts and constexpr, as well as defining a format for reflection metadata.
These goals lead to a few categories of interesting features, which we’ll discuss below.
Standard disclaimers: no, it wouldn’t make sense to enforce this style on existing projects/teams, no, the library is not “production-ready,” and yes, C++ is Bad™ so I considered switching to language X.
Note: this is all pre-modules, so may change soon. CMake recently released support!
C++ compilers are slow, but building your codebase doesn’t have to be. Let’s investigate how MSVC spends its time compiling another project of mine, which is written in a mainstream C++17 style. Including dependencies, it’s about 100k lines of code and takes 20 seconds to compile with optimizations enabled.1
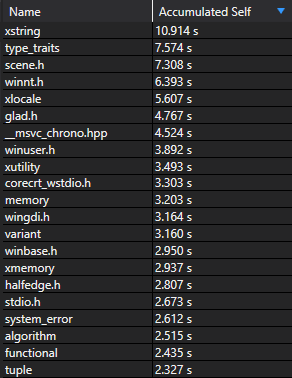
Processing this list of files took up the vast majority of compilation time, but only a handful are actually used in the project—the rest were pulled in to support the STL.
We’ll also find several compilation units that look like this:

Here, including only std::chrono took 75% of the entire invocation.
One would hope that incremental compilation is still fast, but the slowest single compilation unit spent ten seconds in the compiler frontend. Much of that time was spent solving constraints, creating instances, and generating specializations for STL data structures.
The STL’s long compile times can be mitigated by using precompiled headers (or modules…in C++23), but the core issue is simply that the STL is huge.
So, how fast can we go by avoiding it? Here’s my rendering project, which is also roughly 100k lines of code, including rpp and other dependencies. (Click to play.)
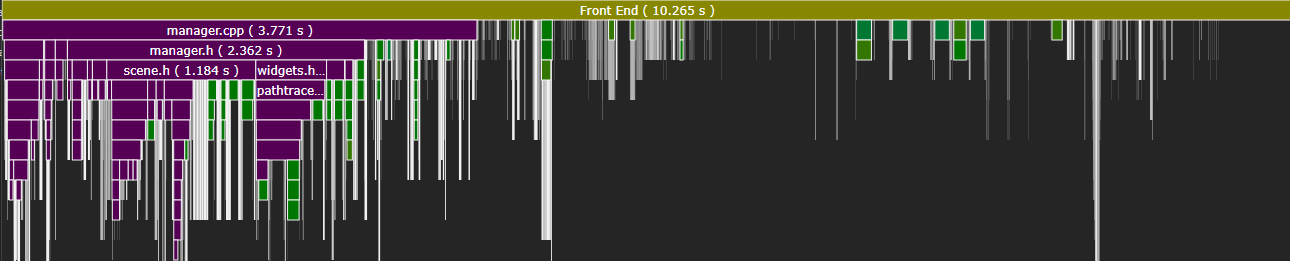
The optimized build completes in under 3 seconds. There’s no trick—I’ve just minimized the amount of code included into each compilation unit. Let’s take a look at where MSVC spends its time:
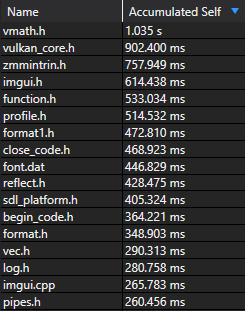
Most of these files come from non-STL dependencies and are actually required by the project. Several arise from rpp, but the worst offender (vmath) only accumulated 1s of work.
Incremental compilation is also much improved: the slowest compilation unit only spent 1.4s in the frontend.
Within each unit, we can see that including base.h (the bulk of rpp) took under 200ms on average.

Of course, this is not a proper benchmark: I’m comparing two entirely separate codebases. Project structure has a large impact on compile times, as does usage code, so your milage may vary. Nevertheless, after working on both projects, I found the decreased iteration time alone to be worth ditching the STL.
You might wonder whether rpp only compiles quickly because it omits most STL features. This is obviously true to some extent: it’s only 10k lines of code, only supports Windows/Linux/x64, and isn’t concerned with backwards compatibility.
However, rpp replicates all of the STL features I actually use.
Implementing the core functionality takes relatively little code, and given some care, we can keep compile times low.
For example, we can still use libc and the Windows/Linux APIs, so long as we relegate their usage to particular compilation unit.2
User code only sees the bare-minimum symbols and types—windows.h need not apply.
OS_Thread sys_start(OS_Thread_Ret (*f)(void*), void* data);
void sys_join(OS_Thread thread);
Unfortunately, the same cannot be said for the STL proper, as (most) generic code must be visible to all compilation units. Hence, rpp re-implements many STL data structures and algorithms. They’re not that hard to compile quickly—STL authors have just never prioritized it.
array.h box.h files.h format.h function.h hash.h heap.h log.h map.h
math.h opt.h pair.h thread.h queue.h rc.h reflect.h rng.h stack.h
string.h tuple.h variant.h vec.h
These two approaches let us entirely eliminate standard headers.
Due to built-in language features, we can’t quite get rid of std::initializer_list and std::coroutine_handle, but the necessary definitions can be manually extracted into a header that does not pull in anything else.
Let’s discuss rpp’s primary data structures.
We will write T and A to denote generic type parameters and allocators, respectively.
The following section will discuss allocators in more detail.
There are five types of pointers, each with different ownership semantics.
Except for raw pointers, all must point to a valid object or be null.
T* is rarely used.
The referenced memory is never owned; there are no other guarantees.
Ref<T> is nearly the same as a raw pointer but removes pointer arithmetic and adds null checks.
Box<T, A> is a uniquely owning pointer, similar to std::unique_ptr.
It may be moved, but not copied, and frees its memory when destroyed.
Rc<T, A> is a non-atomically reference-counted pointer.
The reference count is stored contiguously with the pointed-to object.
It may be moved or copied and frees its memory when the last reference is destroyed.
Arc<T, A> is an atomically reference-counted Rc, similar to std::shared_ptr.
String<A> contains a pointer, a length, and a capacity.
Strings are not null-terminated and may contain null bytes.
There is no “small-string” optimization, so creating a non-empty string always allocates.3
String_View provides a non-owning immutable view of a string, similar to std::string_view.
Most non-destructive string operations are implemented on String_View.
String literals may be converted to String_Views using the _v literal suffix.
String_View message = "foo"_v;
String<> copy = message.string<>();
if(copy.view() == "bar"_v) // ...
Array<T, N> is a fixed-size array of length N.
It’s essentially an rpp-compatible std::array.
Array<i32, 3> int_array{0, 1, 2};
Vec<T, A> is a dynamically-sized array, similar to std::vector.
There is no “small-vector” optimization, so creating a non-empty vector always allocates.4
Vec<i32> int_vec{0, 1, 2};
int_vec.push(3);
int_vec.pop();
Slice<T> is a non-owning immutable view of a contiguous array, similar to std::span.
A Slice may be created from an Array, a Vec, a std::initializer_list, or a raw pointer & length.
Non-destructive functions on arrays take Slice parameters, which abstract over the underlying storage.
This erases (e.g.) the size of the Array or the allocator of the Vec, reducing template bloat.
void print_slice(Slice<i32> slice) {
for(i32 i : slice) info("%", i);
}
Stack<T, A>, Queue<T, A>, and Heap<T, A> are array-based containers with stack, queue, and heap semantics, respectively.
Queue is implemented using a growable circular buffer, and Heap is a flat binary min-heap with respect to the less-than operator.
Stack<i32> int_stack{1, 2, 3};
int_stack.top(); // 3
Queue<i32> int_queue{1, 2, 3};
int_queue.front(); // 1
Heap<i32> int_heap{1, 2, 3};
int_heap.top(); // 1
Map<K, V, A> is an open-addressed hash table with Robin Hood linear probing.
For further discussion of why this is a good choice, see Optimizing Open Addressing.
Map<String_View, i32> int_map{Pair{"foo"_v, 0}, Pair{"bar"_v, 1}};
int_map.insert("baz"_v, 2);
int_map.erase("bar"_v);
for(auto& [key, value] : int_map) info("%: %", key, value);
The implementation is very similar to Optimizing Open Addressing, except that the table also stores key hashes. This improves performance when hashing keys is expensive—particularly for strings.5
Opt<T> is either empty or contains value of type T.
It is not a pointer; it contains a boolean flag and storage for a T.
Optionals are used for error handling, as rpp does not use exceptions.
Opt<i32> int_opt{1};
if(int_opt) info("%", *int_opt);
There is currently no Result<T, E> type, but I plan to add one.
Pair<A, B> contains two values of types A and B.
It supports structured bindings and is used in the implementation of Map.
Pair<i32, f32> pair{1, 2.0f};
i32 one = pair.first;
auto [i, f] = pair;
Tuple<A, B, C, ...> is a heterogeneous product type, which may be accessed via (static) indexing or structured binding.
Tuple<i32, f32, String_View> product{1, 2.0f, "foo"_v};
i32 one = product.get<0>();
auto [i, f, s] = product;
An N-element tuple is represented by a value and an N-1-element tuple. At runtime, this layout is equivalent to a single struct with N fields.
struct { A first; struct { B first; struct { C first; struct {}}}}
The linear structure makes compile-time tuple operations occur in linear time—but I haven’t found this to be an issue in practice. Structuring tuples as binary trees would accelerate compilation, but the code would be more complex.
Variant<A, B, C, ...> is a heterogeneous sum type.
It is superficially similar to std::variant, but has several important differences:
std::monostate.std::bad_variant_access.valueless_by_exception.Variants are accessed via (scuffed) pattern matching: the match method invokes a callable object overloaded for each alternative.
The Overload helper lets the user write a list of (potentially polymorphic) lambdas.
Variant<i32, f32, String_View> sum{1};
sum = 2.0f;
sum.match(Overload{
[](i32 i) { info("Int %", i); },
[](f32 f) { info("Float %", f); },
[](auto) { info("Other"); },
});
Requiring distinct types means a variant can’t represent multiple alternatives of the same type.
We can work around this restriction using the Named helper, but the syntax is clunky.
Variant<Named<"X", i32>, Named<"Y", i32>> sum{Named<"X", i32>{1}};
sum.match(Overload{
[](Named<"X", i32> x) { info("%", x.value); },
[](Named<"Y", i32> y) { info("%", y.value); },
});
Like optionals, variants are not pointers: they contain an index and sufficient storage for the largest alternative.
However, variants also need a way to map the runtime index to a compile-time type.
Given at most eight alternatives, it simply checks the index with a chain of if statements.
Otherwise, it indexes a static table of function pointers, which is generated at compile time.
This introduces an indirect call, but is still relatively fast.
Function<R(A, B, C...)> is a type-erased closure.
It must be provided parameters of types A, B, C, etc., and returns a value of type R.
Function is similar to std::function, but has a few important differences:
std::bad_function_call.std::move_only_function).Functions can be constructed from any callable object with the proper type—in practice, usually a lambda.
Function<void(i32)> print_int = [](i32 i) { info("%", i); };
By default, a Function only has 4 words of storage, so there’s also FunctionN<N, R(A, B, C...)>, which has N words of storage.
In-place storage implies that all functions in a homogeneous collection must have a worst-case size.
If this becomes a problem, you should typically defunctionalize or otherwise restructure your code.
At runtime, functions contain an explicit vtable pointer and storage for the callable object. The vtable is a static array of function pointers generated at compile time. Calling, moving, or destroying the function requires an indirect call—where possible, it’s better to template usage code on the underlying function type.
In rpp, all non-trivial operations should be visible in the source code. This is not generally the case in mainstream C++: most types can be implicitly copied, single-argument constructors introduce implicit conversions, and many operations conditionally allocate memory.
Unlike the STL, rpp data structures cannot be implicitly copied.
To duplicate (most) non-trivial types, you must explicitly call their clone method.
Vec<i32> foo{0, 1, 2};
Vec<i32> bar = foo.clone();
Vec<i32> baz = move(foo);
The Clone concept expresses this capability, allowing generic code to clone supported types.
Additionally, concepts are used to pick the most efficient implementation of clone.
For example, “trivially copyable” types can be copied with memcpy, as seen in Array:
Array clone() const
requires(Clone<T> || Copy_Constructable<T>) {
Array result;
if constexpr(Trivially_Copyable<T>) {
Libc::memcpy(result.data_, data_, sizeof(T) * N);
} else if constexpr(Clone<T>) {
for(u64 i = 0; i < N; i++) result[i] = data_[i].clone();
} else {
for(u64 i = 0; i < N; i++) result[i] = T{data_[i]};
}
return result;
}
Roughly all constructors are marked as explicit, so do not introduce implicit conversions.
I think this is the correct tradeoff, but it has a downside: type inference for template parameters is quite limited.
That means we often have to annotate otherwise-obvious types.
Vec<i32> make_vec(i32 i) {
return Vec<i32>{i}; // Have to write the "<i32>"
}
Compared to previous versions, C++20 has much better native support for compile-time computation.
Hence, rpp does not provide many metaprogramming tools beyond using constexpr, consteval, etc. where possible.
However, it does include a reflection system, which is used to implement a generic printf.
To make a type reflectable, the user creates a specialization of the struct Reflect::Refl.
This may be done manually, or with a helper macro. For example:
struct Data {
Vec<i32> ints;
Vec<f32> floats;
};
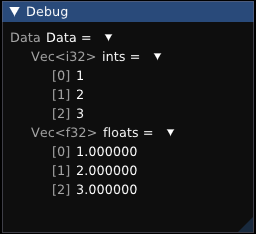
RPP_RECORD(Data, RPP_FIELD(ints), RPP_FIELD(floats));
By default, rpp provides specializations for all built-in types and rpp data structures. Eventually, we’ll get proper compiler support for reflection, but it’s still years away from being widely available.6
The generated reflection data enables operating on types at compile time. For example, we can iterate the fields of an arbitrary record:
struct Print_Field {
template<Reflectable T>
void apply(const Literal& field_name, const T& field_value) {
info("%: %", field_name, field_value);
}
};
Data data;
iterate_record(Print_Field{}, data);
The reflection API includes various other low-level utilities, but it’s largely up to the user to build higher-level abstractions. One example is included: a generic printing system, which is used in the logging macros we’ve seen so far.
Data data{Vec<i32>{1, 2, 3}, Vec<f32>{1.0f, 2.0f, 3.0f}};
info("%", data);
By default, formatting a record will print each field.
Formatting behavior can be customized by specializing Format::Write / Format::Measure, which are provided for all built-in data structures.
Data{ints : Vec[1, 2, 3], floats : Vec[1.000000, 2.000000, 3.000000]}
The implementation is surprisingly concise: it’s essentially an if constexpr branch for each primitive type, plus iterating records/enums.
It’s also easy to extend: for my renderer, I wrote a similar system that generates Dear ImGui layouts for arbitrary types.
In rpp, all data structures are statically associated with an allocator.
Vec<u64, Mdefault> vector;
This approach appears similar to the STL, which also parameterizes data structures over allocators, but is fundamentally different. An rpp allocator is purely a type, not a value, so is fully determined at compile time. That means the specific allocator used by a data structure is part of its type.
By default, all allocations come from Mdefault, which is a thin wrapper around malloc/free that records allocation events.
It starts to get interesting once we allow the user to define new allocators:
using Custom = Mallocator<"Custom">;
Vec<u64, Custom> vector;
Here, Custom still just wraps malloc/free, but its allocation events are tracked under a different name.
Now, if we print allocation statistics:
Allocation stats for [Custom]:
Allocs: 3
Frees: 3
High water: 8192
Alloc size: 24576
Free size: 24576
Printing this data at program exit makes it easy to find memory leaks and provides a high-level overview of where your memory is going.
Tracking heap allocations is useful, but it doesn’t obviously justify the added complexity. More interestingly, rpp data structures also support stack allocation. The rpp stack allocator is a global, thread-local, chunked buffer that is used to implement regions. For further discussion of this design, see Oxidizing OCaml.
Passing the Mregion allocator to a data structure causes it to allocate from the current region.
Allocating region memory is almost free, as it simply bumps the stack pointer.
Freeing memory is a no-op.
Vec<u64, Mregion<R>> local_vector;
Regions are denoted by the Region macro.
Each region lasts until the end of the following scope, at which point all associated allocations are freed.
Region(R) { // R starts here
// Allocate a Vec in R
Vec<u64, Mregion<R>> local_vector;
local_vector.push(1);
local_vector.push(2);
} // R ends here
Unfortunately, regions introduce a new class of memory bugs. Region-local values must not escape their scope, and a region must not attempt to allocate memory associated with a parent. In OCaml or Rust, these properties can be checked at compile time, but not so in C++.
Instead, rpp uses a runtime check to ensure region safety.
When allocating or freeing memory, the allocator checks that the current region has the same brand as the region associated with the allocation.
Brands are named by the user and passed as the template parameter of Mregion.
Region(R0) {
Vec<u64, Mregion<R0>> local_vector;
Region(R1) {
local_vector.push(1); // Region brand mismatch!
}
}
Brands are compile-time constants derived from the region’s source location, so do not introduce any runtime overhead beyond the check itself.
Since C++17, the STL also supports allocator polymorphism—that is, runtime polymorphism.
For example, std::pmr::monotonic_buffer_resource can be used to implement regions, but it incurs an indirect call for every allocation.
Conversely, rpp’s regions are fully determined at compile time.
This design also sidesteps the problem of nested allocators, which is a major pain point in the STL.
Most allocations are either very long-lived, so go on the heap, or very short-lived, so go on the stack. However, it’s occasionally useful to have a middle ground, so rpp also provides pool allocators.
A pool is a simple free-list containing fixed-sized blocks of memory. When the pool is not empty, allocations are essentially free, as they simply pop a buffer off the list. Freeing memory is also trivial, as it pushes the buffer back onto the list.
Passing Mpool to a data structure causes it to allocate from the properly sized pool.
Since pools are fixed-size, Mpool can only be used for “scalar” allocations, i.e. Box, Rc, and Arc.
Box<u64, Mpool> pooled_int{1};
Each size of pool gets its own statistics:
Allocation stats for [Pool<8>]:
Allocs: 2
Frees: 2
High water: 16
Alloc size: 16
Free size: 16
Mpool is similar to std::pmr::synchronized_pool_resource, but is much simpler, as it only supports one block size and does not itself coalesce allocations into chunks.
Currently, each pool is globally shared using a mutex.
This is not ideal, but may be improved by adding thread-local pools and a global fallback.
Parameterizing data structures over allocators provides a lot of flexibility—but it makes all of their operations polymorphic, too.
Regions exacerbate the issue: for example, a function returning a locally-allocated Vec must be polymorphic over all regions.
template<Region R>
Vec<i32, Mregion<R>> make_local_vec() {
return Vec<i32, Mregion<R>>{1, 2, 3};
}
The same friction is present in Rust, where references give rise to lifetime polymorphism. (In fact, brands are a restricted form of lifetimes.) The downside of this approach is code bloat. Due to link-time deduplication, I haven’t run into any issues with binary size, but it could become a problem in larger projects.
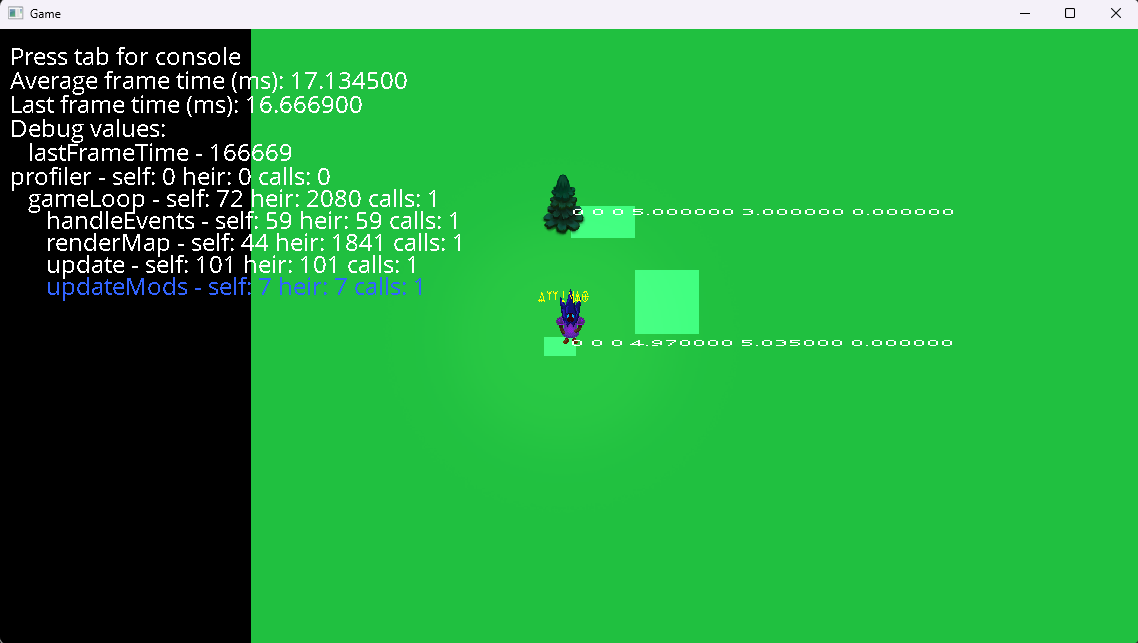
In addition to tracking allocator statistics, rpp records a list of allocation events for each frame.7 This data makes it easy to target an average of zero heap allocations per frame—other than growing the stack allocator.
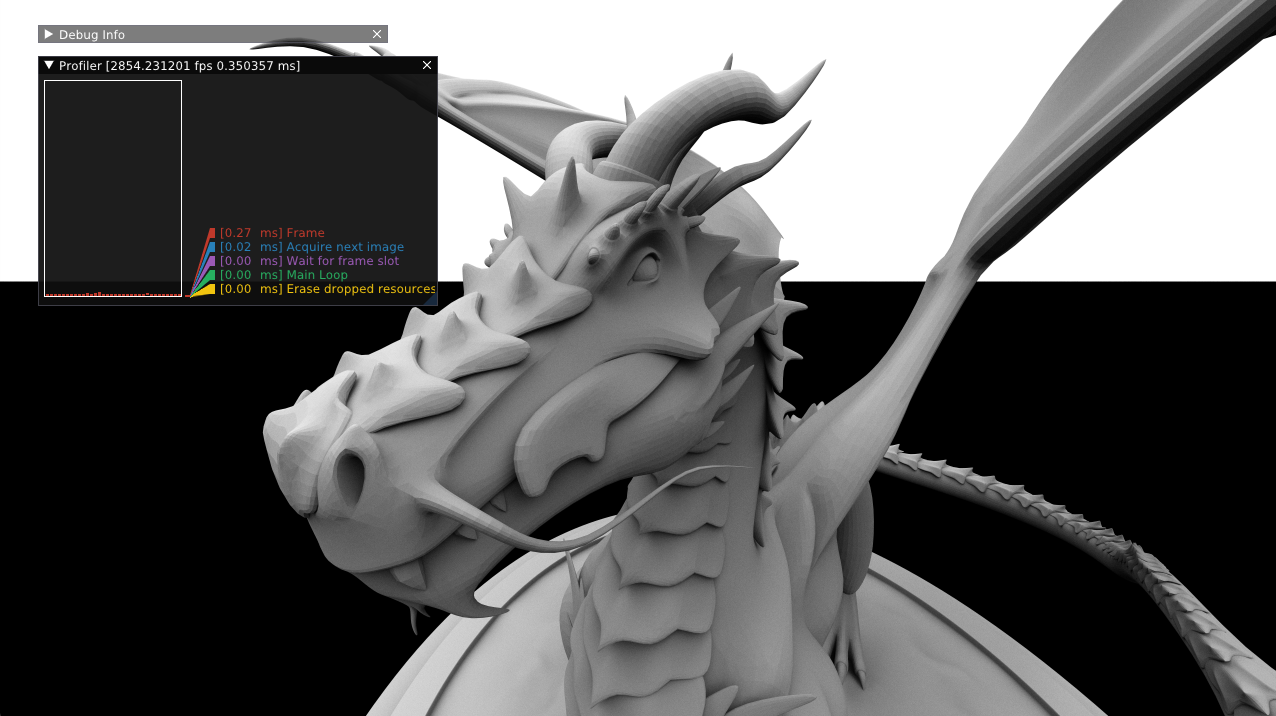
Furthermore, rpp includes a basic tracing profiler.
To record how long a block of code takes to execute, simply wrap it in Trace:
Trace("Trace Me") {
// ...
}
The profiler will compute how many times the block was entered, how much time was spent in the block, and how much time was spent in the block’s children. The resulting timing tree can be traversed by user code, but rpp does not otherwise provide a UI.
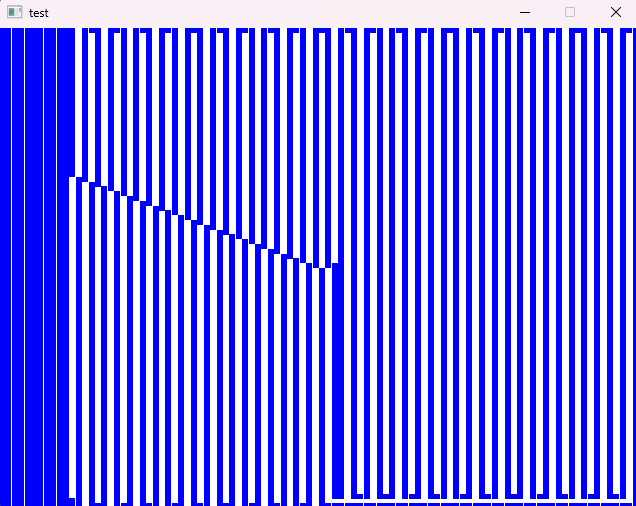
In my renderer, I’ve used rpp’s profile data to graph frame times (based on LegitProfiler):
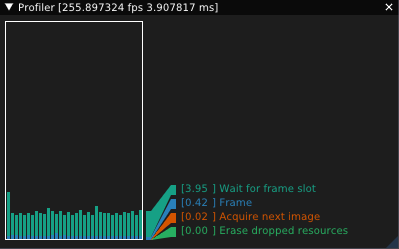
Finally, note that tracing is disabled in release builds.
Coroutines were a somewhat controversial addition to C++20, but I’ve found them to be a good fit for rpp.
Creating an rpp task involves returning an Async::Task<T> from a coroutine:
Async::Task<i32> task1() {
co_return 1;
};
To execute a task on another thread, simply create a thread pool and await pool.suspend().
When a coroutine awaits another task, it will be suspended until the completion of the awaited task.
Async::Task<i32> task2(Async::Pool<>& pool) {
co_await pool.suspend();
co_return co_await task1();
};
It’s possible to write your entire program in terms of coroutines, but it’s often more convenient to maintain a main thread. Therefore, tasks also support synchronous waits:
Async::Pool<> pool;
auto task = task2(pool);
info("%", task.block());
Tasks may be awaited at most once, cannot be copied, and cannot be cancelled after being scheduled.8 These limitations allow the implementation to be quite efficient:
Notably, managing the promise lifetime doesn’t require reference counting. Instead, rpp uses a state machine based on Raymond Chen’s design.
| Task is... | Old Promise State | New Promise State | Action |
|---|---|---|---|
| Created | Start | ||
| Awaited | Done | Done | Resume Awaiter |
| Awaited | Start | Awaiter Address | Suspend Awaiter |
| Completed | Start | Done | |
| Completed | Abandoned | Destroy | |
| Completed | Awaiter Address | Done | Resume Awaiter |
| Dropped | Start | Abandoned | |
| Dropped | Done | Destroy |
Since the awaiter’s address can’t be zero (Start) one (Done) or two (Abandoned), we can encode all states in a single word and perform each transition with a single atomic operation. Additionally, we can use symmetric transfer to resume tasks without requeuing them.
Currently, the scheduler does not support work stealing, prioritization, or CPU affinity, so blocking on another task can deadlock. I plan to add support for these features in the future.
As seen in many other languages, coroutines are also useful for asynchronous I/O. Therefore, the rpp scheduler supports awaiting platform-specific events. Its design is roughly based on coop.
Only basic support for async file I/O and timers is included, but creating custom I/O methods is easy:
Task<IO> async_io(Pool<>& pool) {
HANDLE handle = /* Start an IO operation */;
co_await pool.event(Event::of_sys(handle));
co_return /* The result */;
}
In my renderer, this system enables awaitable GPU tasks based on VK_KHR_external_fences.
co_await vk.async(pool, [](Vk::Commands& commands) {
// Add GPU work to the command buffer
});
Despite compilers having supported coroutines for several years, I still ran into multiple compiler bugs while implementing rpp. This suggests that coroutines are still not widely used, or I imagine the bugs would have been fixed by now.
In particular, MSVC 19.37 exhibits a bug that makes symmetric transfer unsafe, so it’s currently possible for the rpp scheduler to stack overflow on Windows.
As of Jan 2024, a fix is pending release by Microsoft.
I ran into a similar bug in clang, but didn’t track it down precisely because updating to clang-17 fixed the issue.
This may seem like a lot of work that would be better spent transitioning to Rust. Much of rpp is directly inspired by Rust—even the name—but I haven’t been convinced to switch just yet. The kind of projects I work on (i.e. graphics & games) tend to be both borrow-checker-unfriendly and do not primarily suffer from memory or concurrency issues.
That’s not to say these kind of bugs never come up, but I find debuggers, sanitizers, and profiling sufficient to fix issues and prevent regressions. I would certainly prefer these bugs to be caught at compile time, but I haven’t found the language overhead of Rust to be obviously worth it—the painful bugs come from GPU code anyway! Of course, it might be a different story if I wrote security-critical programs.
What has really held me back is simply that the Rust compiler is slow—but now that the parallel frontend has landed, I may reconsider. I would also concede that Rust is the better language to start learning in 2024.
Jai prioritizes many of the same goals as rpp. I sure would like to use it, but it’s been nine years and I still don’t have a copy of the compiler.
In the past, I’ve written a lot of C-style C++, including the first version of rpp (unnamed at the time). In retrospect, I don’t think this style is a great choice, unless you’re very disciplined about not using C++ features. Introducing even a small amount of C++isms leads to a lot of poor interactions with C-style code. Overall, I’d say it’s better to return to plain C.
That said, rpp is obviously influenced by this style: it doesn’t use exceptions, RTTI, multiple/virtual inheritance, or the STL. However, it does make heavy use of templates.
C
I’ve also written a fair amount of C, and I’d say it’s still a good choice for OS-adjacent work. However, I rarely need to think about topics like binary size, inline assembly, or ABI compatibility, so I’d rather have (e.g.) real language support for generics. Plus, at least where available, Rust is often a better choice.
I haven’t written much D, but from what I’ve seen, it’s a pretty sensible redesign of C++. Many of the features that interact poorly in C++ work well in D. However, there’s also the garbage collector—it can be disabled, but you lose out on a lot of library features. Overall, I think D suffers from the problem of being “only” moderately better than C++, which isn’t enough to justify rebuilding the ecosystem.
I tried Odin in 2017, but it wasn’t sufficiently stable at the time. It appears to be in a good state today—and certainly improves on C for application programming—but I think it suffers from the same problem that D does relative to C++.
I feel obligated to mention OCaml, since I now use it professionally, even for systems programming tasks. Modes, unboxed types, and domains are starting to make OCaml very viable for systems-with-incremental-concurrent-generational-GC projects—but it’s not yet a great fit for games/graphics programming.
I would particularly like to see an ML-family language without a GC (maybe along the lines of Koka), but not so imperative/object oriented as Rust.
Zig, Nim, Go, C#, F#, Haskell, Beef, Vale, Java, JavaScript, Python, Crystal, Lisp
I’ve learned about each these languages to some small extent, but none seem sufficiently compelling for my use cases. (Except maybe Zig, which scares me.)
The 100k LOC do not include the STL itself. Benchmarked on an AMD 5950X @ 4.4GHz, MSVC 19.38.33129, Windows 11 10.0.22631. ↩
Unfortunately, this makes the implementations unavailable for inlining. However, I’m prioritizing compile times, and link-time optimization can make up for it. ↩
Adding the small-string optimization only makes sense if it happens to accelerate an existing codebase.
It causes strings’ allocation behavior to depend on their length, resulting in less predictable performance.
Further, if your program creates a lot of small, heap-allocated String<>s, you should ideally refactor it to use String_View, the stack allocator, or a custom interned string representation. ↩
(For the same reasons as strings.) ↩
It also stores hashes alongside integer keys, which doesn’t help. I’ll fix this eventually. ↩
Of course, this data could be generated by a separate meta-program or a compiler plugin, but I haven’t found the additional complexity to be worth it. ↩
Assuming your program is long-running and has a natural frame delineation. Otherwise, the entire execution is traced under one frame. ↩
Because tasks may only be awaited once, they do not support co_yield. ↩

I first encountered programming sometime around 2010, when I was 9 years old.
I can’t recall precisely how or why I got started, but I wrote my first programs in TI-BASIC, meticulously entering each symbol into my TI-83 calculator. They computed simple algebraic expressions that I used to do math problems.
I was fascinated by video games, so after learning how to poll for input, I created Catch the θ. The player would move an ‘I’ character up and down to catch falling ‘θ’ characters. Each new ‘θ’ would fall faster than the last, until it became impossible to catch them all. I soon discovered you could transfer programs between TI calculators, resulting in a new source of distraction for our math class.
The game looked like this:
LIVES: 3 SCORE: 3
I
θ
Around the same time, I got my first personal computer: a big Gateway laptop with a first-gen Intel i3 and 4GB DDR3. Previously, I had only used my parents’ old iMac G3, on which I learned to type, used the AppleWorks programs, and played Mac OS 9’s limited selection of games.1

My new laptop, on the other hand, ran the recently released Windows 7. Windows opened up a whole new world of software I could download from the internet.

I somehow ended up with an IDE called Just BASIC, in which I wrote a few more utilities and text-based games. I only remember one: a “HiLo” game where the player would find a number via binary search.2
Eventually, I wanted to make a game with graphics, so I downloaded GameMaker 8. After following the tutorials, I used the visual scripting language to make a couple games, but never really finished anything. I did, however, write an essay about game development, in which I stated that 3D graphics was “very hard” for amateurs.
Up until this point, I had been more interested in making physical systems than programming—I spent a lot of time on LEGOs, domino runs, and Rube Goldberg machines. Programming something of comparable complexity on my own was still out of reach.
My interests started to converge when I discovered Minecraft upon its release in late 2011. It was one of the first popular building games, and quickly became a mainstay for me. By version 1.2, I was exploring mods that added technology & automation and hosting servers for friends.3
I soon got a desktop computer: a Gateway mid-tower with an i5-2320 and 8GB DDR3. This encouraged me to continue programming, but I didn’t learn Java—the internet claimed Minecraft’s mediocre performance was due to its choice of language.
Instead, I embarked on learning the lingua franca of game development: C++. I started with Dev-C++ 4.9.9.
I can’t remember much from this period, but I believe I first learned C-with-classes style C++ from an online course. Presumably, I then wrote some slightly bigger programs—but I have no record of them, so I must not have gotten very far.
At some point, I got stuck trying to get Allegro to link properly. Some things never change.
This is the first year from which any code is preserved. In school, I took a robotics class, where we used RobotC to control LEGO Mindstorms robots. The programs were simple and messy, including line following and maze solving (if you can call it that).

Outside of school, I acquired an Arduino Uno and did some small projects in C. Judging from files I still have lying around, I made a binary clock, as well as Catch the LED, a game where the player would try to press a button just as a sequence of lights passed a central LED.

I also upgraded the desktop with a GTX 650—to run minecraft shaders, obviously.
I started making more progress with C++, eventually learning C++11 features and switching to Visual Studio. Thanks to the Lazy Foo tutorials, I was able to successfully link SDL and write some graphical programs.
For reasons unknown, I then decided it was time to learn Java. After going through another online course, I used Eclipse to write some more advanced programs, including a matrix calculator/linear solver, a Lorentz transform calculator, and a Pong clone.

At this point, I started spending a lot of time reading articles and watching YouTube videos on technical topics.
I discovered cryptocurrencies and set up my GPU to mine Dogecoin (what else?) for a few weeks. Too bad I lost the wallet—it’d be worth a whole $200 today.

In late 2014, I happened upon one of Jonathan Blow’s streams discussing Jai, a programming language for games. I recall being particularly impressed by the compile-time code execution demo, which seemed so much better than inscrutable C++ templates. More importantly at the time, he mentioned Handmade Hero, Casey Muratori’s new series on creating a game from scratch.
It was just what I wanted to learn—the details of how complex programs actually worked.
I followed Handmade Hero for a few months, learning a lot about low-level programming and operating systems.4 I attempted to follow along with the code, but didn’t have sufficient free time to keep it up indefinitely. Still, the series had a lasting impact on my approach to programming. I learned how to understand programs at multiple levels of abstraction, as well as the practice of semantic compression.
That summer, I took my first formal Computer Science course at the local university. It was an introduction to programming in C++, which I found quite boring.
I built my first computer, scouring the internet for deals and putting together an i7-5820k, GTX 970, 16GB DDR4 build for ~$1000.5 I repurposed the old hardware as a media / game server running Unraid.

In the fall, I took a second CS course, but it wasn’t much better. More importantly, I started teaching programming. I ran a weekly elective class, teaching yet another introduction to programming in C++. The first semester covered the basics: control flow, functions, IO, memory management, classes, and sorting. For sample projects, I wrote a square root calculator, maze escape game, and BS poker card game.
Outside of school, I started using Sublime Text in conjunction with the Visual Studio debugger. I learned how to use Git and pushed my first project to GitHub. It was my most complex program yet: a text-based RPG engine that would interpret a file containing a tree of locations/prompts. The code was rather disorganized and probably leaked memory, but it successfully performed recursive-descent parsing and tree traversal.
At some point, I learned a bit of Python, but didn’t stick with it.
Inspired by Handmade Hero, I started working on my own 2D game engine. It wasn’t totally from scratch—I used SDL2 and the C++ STL. I would work on it for the rest of the year.
The “engine” part mostly consisted of wrappers around SDL2 and associated libraries, but also included a sprite renderer, a chunked world system, hot reloading, text rendering, profiling features, and (buggy) collisions.
I taught a second semester of programming, this time covering more advanced C++ topics like operator overloading, basic data structures, templates, and OOP. I started converting the notes I had written into a website, which gets a fair amount of traffic to this day. I wrote a “Simple Drawing Library” and used it to demonstrate DFS/BFS.
In the fall, I took Data Structures, which was more interesting than the introductory courses. I taught a third semester, this time focusing on SDL2 and game programming patterns. I wrote my own condensed version of the Lazy Foo tutorials I had followed in years prior.
I got tired of the 2D engine and embarked on learning 3D rendering. I started learning OpenGL 3.3 from learnopengl.com and found it quite fun. At the time, I was taking calculus III, so I started working on a 3D graphing program. I also discovered Dear ImGui, which I’ve used ever since.
I would occasionally add features for ~1.5 years, and the grapher would became my first program that anyone else actually used.
In spring, I took a “Math for Computer Science” (i.e. logic and proofs) class, which was new and interesting. I played The Witness, which doesn’t directly relate to programming, but greatly influenced how I think about game design.

I taught a fourth semester, this time covering data structures and C++11 topics. I stopped updating the website, but created lessons on stacks, queues, lists, heaps, balanced trees, hash maps, graphs, threading, smart pointers, move semantics, exceptions, and basic functional programming.
In the summer, I began a larger project: a Minecraft-inspired 3D voxel engine called Exile. This time, it was from scratch: I wrote my own data structures, Win32 and Linux platform code, ImGui, and OpenGL 4 renderer.
The project started in the Odin programming language, but I quickly switched back to C++ since the Odin compiler wasn’t stable at the time. I also tried streaming my work on Twitch, but never consistently. Finally, I started tracking my ever-growing repository of bookmarks on GitHub.
I would work on Exile sporadically for the next several years, eventually rewriting it multiple times and evolving it into the pure-rendering project I’m working on today.
I did a month-long internship with a local mobile gaming startup, where I wrote some promotional Facebook games in Javascript. I don’t think they amounted to anything, but I got paid (a bit) for programming.
In the fall, I started supervising a few group projects instead of teaching new content. I took Computer Graphics, where (yet again) I already knew a good deal of the content—but I enjoyed it anyway. I made a solar system simulator, a physics-based pinball game, and a chunk-based voxel renderer that I later used in Exile.

During spring/summer, I spent a lot of time working on Exile.
I learned more advanced rendering techniques, including deferred lighting, ambient occlusion, and environment maps. I designed a memory efficient rendering pipeline for voxel data, and wrote a libclang-based metaprogram that generated reflection data.
I wrote my first three blog posts on Exile’s hot reloading, reflection, and voxel meshing systems.
I then left home to attend university. I started taking many technical courses, but I’ll only be mentioning those with significant programming projects. It started with another round of discrete math and data structures, which were a big step up in difficulty.

My friend and I participated in a hackathon, where we made a visualization app for high-dimensional machine learning data.
I also started using VSCode, learned \(\LaTeX\), and basically never handwrote anything again.
In spring, I took a functional programming class, which I found pretty elegant and intuitive. The class was taught in SML, exposing me to a language with a coherent design. I continued using C++, but started applying more functional programming techniques.

In summer, I interned at NVIDIA, working on some automated OpenGL benchmarking tools. It turned out there wasn’t much work to do, so I spent much of my time working on a ray tracer based on Ray Tracing in One Weekend, as well as Exile. I found and reported a miscompilation bug in the Visual Studio compiler.
In fall, I took several more classes.
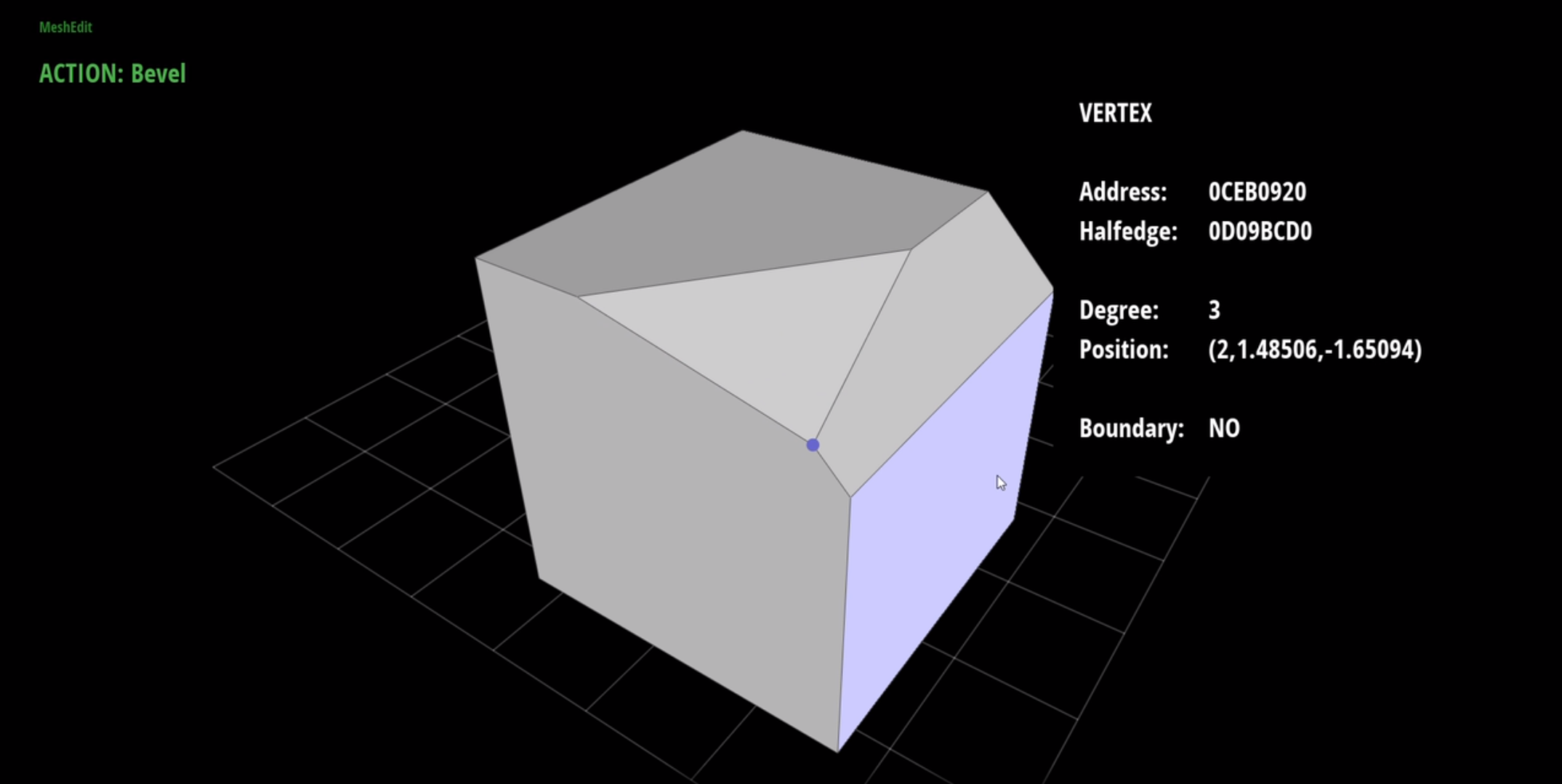
I particularly enjoyed graphics, but was frustrated with the course’s out-of-date OpenGL 2 codebase, Scotty3D. Therefore, I applied to become a teaching assistant for the course, and began work on a new version of Scotty3D in modern C++17 and OpenGL 4.
In spring, I took a course on operating systems, where (along with a partner) I wrote a bare-metal Sokoban game, a user-space threading library, and an x86 kernel, all from scratch in C. Our kernel ran on real hardware, supporting virtual memory, preemptive multitasking, and concurrent syscalls. The course taught me a lot about concurrency and system design, though our final product was certainly not entirely concurrency-safe.6
In the summer, I interned at Apple, working on more GPU benchmarking tools. Unfortunately, this was the summer of COVID, so my project was derailed and I again didn’t end up with much work to do. Hence, I spent a lot of time on Scotty3D. By the end of the summer, it was ready to support three of the four major assignments.
That fall, we released the new version—I had to fix many bugs, but overall it was a big hit. Students were able to produce much cooler results than previous years.
I also took a compilers course, where (along with a partner) I wrote a compiler for the C0 language. We implemented the compiler in Rust, which I would describe as a redesign of C++ without (most of) the insanity.7 Much of the work was in the compiler backend, which supported SSA, SCCP, register allocation, x86 code generation, and fork/join parallelism.

Finally, I started writing a new version of Exile from scratch, this time using Vulkan and modern C++17. Keeping with the theme, I again started by writing my own standard library. To learn Vulkan, I went through the Vulkan Tutorial, which was useful, but I later realized it contained some bad advice.
I built a new computer: a compact ITX system with a Ryzen 5950X, RTX 3090, and 32GB DDR4. The GPU shortage was in full swing, so I borrowed the GPU from one of the graphics PhD students—ostensibly for research purposes—and later replaced it with an RTX 3080ti.

In spring, I took several more classes:
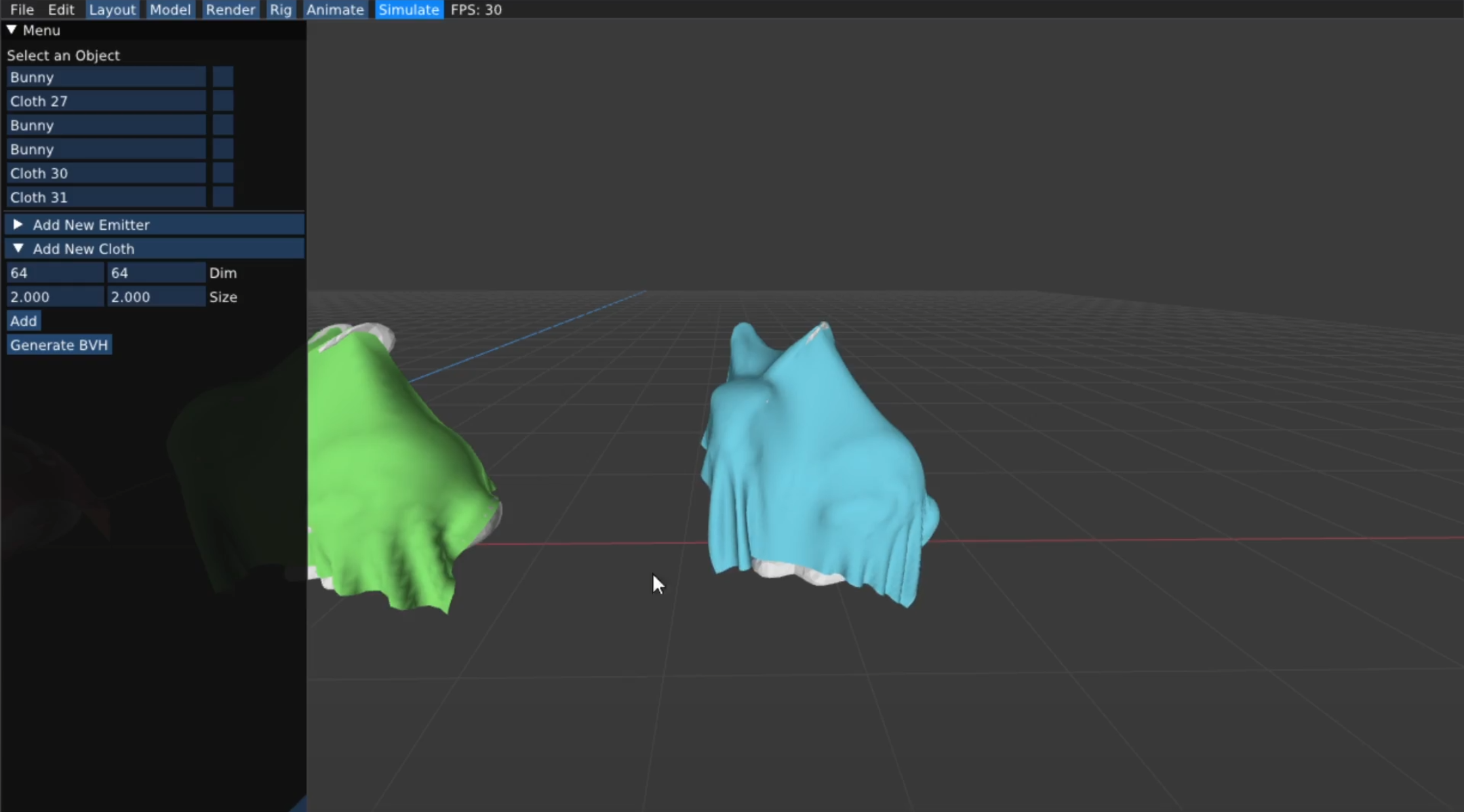

In the summer, I interned at Jane Street, where I learned OCaml and gained more practical experience with functional programming. I worked on an autocompletion engine for S-expressions, as well as APIs for risk management.

In the fall, I took a programming languages course (also in OCaml), where I learned more about type systems, static analysis, and theorem provers. I also took “deep learning systems,” where I implemented my own version of PyTorch in Python and CUDA. I hadn’t done any formal machine learning courses, so I got to learn a lot about both deep learning and its practical implementation.
I did another research assistantship, where I worked on sampling strategies for differentiable rendering in Mitsuba. I didn’t really have enough time for this project, so it didn’t amount to much.
Up until now, I had been a TA for the graphics course. This semester, I switched to game programming, which was pretty fun.
Finally, I graduated. With my newfound free time, I decided to restart my blog. I wrote a couple short posts on that compiler bug from 2019 and hamming codes.
In the spring, I felt pretty burnt out after seven semesters and three summers of work, so didn’t do much of anything (other than finally getting to Grandmaster in Overwatch).
I eventually wrote a longer, interactive post about 3D rotations and the exponential map. The response greatly exceeded my expectations—it was my first post to get a lot of traffic, mostly from Hacker News and Twitter.

In the summer, I did another brief stint as a research assistant working on additional updates to Scotty3D. We wrote a new instanced scene graph, a test suite for the assignments, a custom file format, and integrated the remaining major assignment into the codebase.
I wrote another interactive post on differentiable programming, which received an honorable mention in the Summer of Math Exposition.

I did some more work on Exile, rewriting the Vulkan abstractions and using RTX hardware to dynamically render huge amounts of cubes at high frame rates.

I then became a full time software engineer on Jane Street’s compilers team. I began working on profiling and optimization tools, as well as learning more OCaml and functional programming theory.
I wrote another post on neural graphics primitives, the first to cover a research topic.
In the winter, I didn’t do much programming, but briefly worked on a puzzle game concept with a friend.

In spring, I wrote posts on spherical integration and open addressed hash tables, which also became relatively popular.

For work, I wrote a series of articles covering the addition of modes to the OCaml type system. We’re slowly making OCaml more akin to Rust, so I titled the series Oxidizing OCaml.
In the summer, I started contributing primarily to the OCaml compiler itself. I implemented support for SIMD types & operations, as well as other additions to the x86 backend.
I wrote my longest post yet on functional analysis, which received another honorable mention in the Summer of Math Exposition.
Functions are Vectors took so long (likely 100+ hours) that I lost motivation to write anything else until the post you’re reading right now.
Instead, I did some more programming: I ripped out the core of Exile and started a new project focused on real-time path tracing. I did another pass on the Vulkan abstraction layer, which I think is finally in a good state. It covers all the fancy features you’re supposed to use in Vulkan, like multiple frames in flight, multithreaded command buffer recording, async compute and transfer queues, dynamic rendering, and custom allocators.
For reasons of masochism, I then decided to rewrite my C++ standard library *again*, this time in C++20. I think it’s also finally in a pretty good state, so I put the current version on GitHub.
And that brings us to the present. I’m working on a post covering the design principles behind the library, as well as how I got it to compile in 100ms per invocation.
I’m part of the first generation to grow up with the Web, but the last to remember it before the rise of smartphones. In some respects, this meant the late 2000s was the easiest time in history to get started in computing.
You may have noticed this post doesn’t reference any textbooks, nor any personal mentors (though it does include a degree). That’s because I was able to learn primarily from the internet, which wasn’t really feasible for previous generations. However, the leap from using computers to modifying them was still small: doing anything interesting required delving into desktop computing, which lead to programming.
Now, users can get by without learning to type, let alone program—so most never do. On the other hand, online resources are more accessible than ever. The pandemic heralded a big increase in the amount of university-level content online, and I expect that trend to continue. Going beyond YouTube and its ilk, students of the 2020s will have access to LLMs, which can (arguably) already function as search engine and tutor.
We’ll see how it turns out.
See Roller Coaster Tycoon 3, Marble Blast Gold, and Enigmo. ↩
Did I watch this video? I have no idea. ↩
See IndustrialCraft, BuildCraft, RedPower, ComputerCraft, and Railcraft. Remember Hamachi? ↩
Don’t start here if you want to finish a game. It was great for learning systems programming, though. ↩
The human eye can’t see more than 3.5GB anyway. ↩
Arguably, (unstructured) concurrency is the only really difficult problem in programming. Help from the compiler is sorely needed. ↩
I think Rust is a good language, but I’ve since avoided it because I value short compile times and don’t work on anything security-critical. I also do borrow-checker-unfriendly things (e.g. using Vulkan) that are annoying in Rust. However, I may return to it now that the parallel frontend has landed. ↩















Prerequisites: introductory linear algebra, introductory calculus, introductory differential equations.
This article received an honorable mention in 3Blue1Brown’s Summer of Math Exposition 3!
Vectors are often first introduced as lists of real numbers—i.e. the familiar notation we use for points, directions, and more.
You may recall that this representation is only one example of an abstract vector space. There are many other types of vectors, such as lists of complex numbers, graph cycles, and even magic squares.
However, all of these vector spaces have one thing in common: a finite number of dimensions. That is, each kind of vector can be represented as a collection of \(N\) numbers, though the definition of “number” varies.
If any \(N\)-dimensional vector is essentially a length-\(N\) list, we could also consider a vector to be a mapping from an index to a value.
\[\begin{align*} \mathbf{v}_1 &= x\\ \mathbf{v}_2 &= y\\ \mathbf{v}_3 &= z \end{align*}\ \iff\ \mathbf{v} = \begin{bmatrix}x \\ y \\ z\end{bmatrix}\]What does this perspective hint at as we increase the number of dimensions?
Dimensions
In higher dimensions, vectors start to look more like functions!
Of course, a finite-length vector only specifies a value at a limited number of indices. Could we instead define a vector that contains infinitely many values?
Writing down a vector representing a function on the natural numbers (\(\mathbb{N}\))—or any other countably infinite domain—is straightforward: just extend the list indefinitely.
This vector could represent the function \(f(x) = x\), where \(x \in \mathbb{N}\).1
Many interesting functions are defined on the real numbers (\(\mathbb{R}\)), so may not be representable as a countably infinite vector. Therefore, we will have to make a larger conceptual leap: not only will our set of indices be infinite, it will be uncountably infinite.
That means we can’t write down vectors as lists at all—it is impossible to assign an integer index to each element of an uncountable set. So, how can we write down a vector mapping a real index to a certain value?
Now, a vector really is just an arbitrary function:
Precisely defining how and why we can represent functions as infinite-dimensional vectors is the purview of functional analysis. In this post, we won’t attempt to prove our results in infinite dimensions: we will focus on building intuition via analogies to finite-dimensional linear algebra.
Formally, a vector space is defined by choosing a set of vectors \(\mathcal{V}\), a scalar field \(\mathbb{F}\), and a zero vector \(\mathbf{0}\). The field \(\mathbb{F}\) is often the real numbers (\(\mathbb{R}\)), complex numbers (\(\mathbb{C}\)), or a finite field such as the integers modulo a prime (\(\mathbb{Z}_p\)).
Additionally, we must specify how to add two vectors and how to multiply a vector by a scalar.
\[\begin{align*} (+)\ &:\ \mathcal{V}\times\mathcal{V}\mapsto\mathcal{V}\\ (\cdot)\ &:\ \mathbb{F}\times\mathcal{V} \mapsto \mathcal{V} \end{align*}\]To describe a vector space, our definitions must entail several vector space axioms.
In the following sections, we’ll work with the vector space of real functions. To avoid ambiguity, square brackets are used to denote function application.
Adding functions corresponds to applying the functions separately and summing the results.
This definition generalizes the typical element-wise addition rule—it’s like adding the two values at each index.
\[f+g = \begin{bmatrix}f_1 + g_1 \\ f_2 + g_2 \\ \vdots \end{bmatrix}\]Multiplying a function by a scalar corresponds to applying the function and scaling the result.
This rule similarly generalizes element-wise multiplication—it’s like scaling the value at each index.
\[\alpha f = \begin{bmatrix}\alpha f_1 \\ \alpha f_2 \\ \vdots \end{bmatrix}\]Given these definitions, we can now prove all necessary vector space axioms. We will illustrate the analog of each property in \(\mathbb{R}^2\), the familiar vector space of two-dimensional arrows.
Therefore, we’ve built a vector space of functions!3 It may not be immediately obvious why this result is useful, but bear with us through a few more definitions—we will spend the rest of this post exploring powerful techniques arising from this perspective.
Unless specified otherwise, vectors are written down with respect to the standard basis. In \(\mathbb{R}^2\), the standard basis consists of the two coordinate axes.
Hence, vector notation is shorthand for a linear combination of the standard basis vectors.
Above, we represented functions as vectors by assuming each dimension of an infinite-length vector contains the function’s result for that index. This construction points to a natural generalization of the standard basis.
Just like the coordinate axes, each standard basis function contains a \(1\) at one index and \(0\) everywhere else. More precisely, for every \(\alpha \in \mathbb{R}\):
Ideally, we could express an arbitrary function \(f\) as a linear combination of these basis functions. However, there are uncountably many of them—and we can’t simply write down a sum over the reals. Still, considering their linear combination is illustrative:
\[\begin{align*} f[x] &= f[\alpha]\mathbf{e}_\alpha[x] \\ &= f[1]\mathbf{e}_1[x] + f[2]\mathbf{e}_2[x] + f[\pi]\mathbf{e}_\pi[x] + \dots \end{align*}\]If we evaluate this “sum” at \(x\), we’ll find that all terms are zero—except \(\mathbf{e}_x\), making the result \(f[x]\).
Now that we can manipulate functions as vectors, let’s start transferring the tools of linear algebra to the functional perspective.
One ubiquitous operation on finite-dimensional vectors is transforming them with matrices. A matrix \(\mathbf{A}\) encodes a linear transformation, meaning multiplication preserves linear combinations.
\[\mathbf{A}(\alpha \mathbf{x} + \beta \mathbf{y}) = \alpha \mathbf{A}\mathbf{x} + \beta \mathbf{A}\mathbf{y}\]Multiplying a vector by a matrix can be intuitively interpreted as defining a new set of coordinate axes from the matrix’s column vectors. The result is a linear combination of the columns:
When all vectors can be expressed as a linear combination of \(\mathbf{u}\), \(\mathbf{v}\), and \(\mathbf{w}\), the columns form a basis for the underlying vector space. Here, the matrix \(\mathbf{A}\) transforms a vector from the \(\mathbf{uvw}\) basis into the standard basis.
Since functions are vectors, we could imagine transforming a function by a matrix. Such a matrix would be infinite-dimensional, so we will instead call it a linear operator and denote it with \(\mathcal{L}\).
This visualization isn’t very accurate—we’re dealing with uncountably infinite-dimensional vectors, so we can’t actually write out an operator in matrix form. Nonetheless, the structure is suggestive: each “column” of the operator describes a new basis function for our functional vector space. Just like we saw with finite-dimensional vectors, \(\mathcal{L}\) represents a change of basis.
So, what’s an example of a linear operator on functions? You might recall that differentiation is linear:
\[\frac{\partial}{\partial x} \left(\alpha f[x] + \beta g[x]\right) = \alpha\frac{\partial f}{\partial x} + \beta\frac{\partial g}{\partial x}\]It’s hard to visualize differentiation on general functions, but it’s feasible for the subspace of polynomials, \(\mathcal{P}\). Let’s take a slight detour to examine this smaller space of functions.
\[\mathcal{P} = \{ p[x] = a + bx + cx^2 + dx^3 + \cdots \}\]We typically write down polynomials as a sequence of powers, i.e. \(1, x, x^2, x^3\), etc. All polynomials are linear combinations of the functions \(\mathbf{e}_i[x] = x^i\), so they constitute a countably infinite basis for \(\mathcal{P}\).4
This basis provides a convenient vector notation:
Since differentiation is linear, we’re able to apply the rule \(\frac{\partial}{\partial x} x^n = nx^{n-1}\) to each term.
We’ve performed a linear transformation on the coefficients, so we can represent differentiation as a matrix!
\[\frac{\partial}{\partial x}\mathbf{p} = \begin{bmatrix}0 & 1 & 0 & 0 & \cdots\\ 0 & 0 & 2 & 0 & \cdots\\ 0 & 0 & 0 & 3 & \cdots\\ \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}\begin{bmatrix}a\\ b\\ c\\ d\\ \vdots\end{bmatrix} = \begin{bmatrix}b\\ 2c\\ 3d\\ \vdots\end{bmatrix}\]Each column of the differentiation operator is itself a polynomial, so this matrix represents a change of basis.
\[\frac{\partial}{\partial x} = \begin{bmatrix} \vert & \vert & \vert & \vert & \vert & \\ 0 & 1 & 2x & 3x^2 & 4x^3 & \cdots \\ \vert & \vert & \vert & \vert & \vert & \end{bmatrix}\]As we can see, the differentiation operator simply maps each basis function to its derivative.
This result also applies to the larger space of analytic real functions, which includes polynomials, exponential functions, trigonometric functions, logarithms, and other familiar names. By definition, an analytic function can be expressed as a Taylor series about \(0\):
\[f[x] = \sum_{n=0}^\infty \frac{f^{(n)}[0]}{n!}x^n = \sum_{n=0}^\infty \alpha_n x^n\]Which is a linear combination of our polynomial basis functions. That means a Taylor expansion is essentially a change of basis into the sequence of powers, where our differentiation operator is quite simple.5
Matrix decompositions are arguably the crowning achievement of linear algebra. To get started, let’s review what diagonalization means for a \(3\times3\) real matrix \(\mathbf{A}\).
A vector \(\mathbf{u}\) is an eigenvector of the matrix \(\mathbf{A}\) when the following condition holds:
The eigenvalue \(\lambda\) may be computed by solving the characteristic polynomial of \(\mathbf{A}\). Eigenvalues may be real or complex.
The matrix \(\mathbf{A}\) is diagonalizable when it admits three linearly independent eigenvectors, each with a corresponding real eigenvalue. This set of eigenvectors constitutes an eigenbasis for the underlying vector space, indicating that we can express any vector \(\mathbf{x}\) via their linear combination.
To multiply \(\mathbf{x}\) by \(\mathbf{A}\), we just have to scale each component by its corresponding eigenvalue.
Finally, re-combining the eigenvectors expresses the result in the standard basis.
Intuitively, we’ve shown that multiplying by \(\mathbf{A}\) is equivalent to a change of basis, a scaling, and a change back. That means we can write \(\mathbf{A}\) as the product of an invertible matrix \(\mathbf{U}\) and a diagonal matrix \(\mathbf{\Lambda}\).
Note that \(\mathbf{U}\) is invertible because its columns (the eigenvectors) form a basis for \(\mathbb{R}^3\). When multiplying by \(\mathbf{x}\), \(\mathbf{U}^{-1}\) converts \(\mathbf{x}\) to the eigenbasis, \(\mathbf{\Lambda}\) scales by the corresponding eigenvalues, and \(\mathbf{U}\) takes us back to the standard basis.
In the presence of complex eigenvalues, \(\mathbf{A}\) may still be diagonalizable if we allow \(\mathbf{U}\) and \(\mathbf{\Lambda}\) to include complex entires. In this case, the decomposition as a whole still maps real vectors to real vectors, but the intermediate values become complex.
So, what does diagonalization mean in a vector space of functions? Given a linear operator \(\mathcal{L}\), you might imagine a corresponding definition for eigenfunctions:
\[\mathcal{L}f = \psi f\]The scalar \(\psi\) is again known as an eigenvalue. Since \(\mathcal{L}\) is infinite-dimensional, it doesn’t have a characteristic polynomial—there’s not a straightforward method for computing \(\psi\).
Nevertheless, let’s attempt to diagonalize differentiation on analytic functions. The first step is to find the eigenfunctions. Start by applying the above condition to our differentiation operator in the power basis:
\[\begin{align*} && \frac{\partial}{\partial x}\mathbf{p} = \psi \mathbf{p} \vphantom{\Big|}& \\ &\iff& \begin{bmatrix}0 & 1 & 0 & 0 & \cdots\\ 0 & 0 & 2 & 0 & \cdots\\ 0 & 0 & 0 & 3 & \cdots\\ \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}\begin{bmatrix}p_0\\ p_1\\ p_2\\ p_3\\ \vdots\end{bmatrix} &= \begin{bmatrix}\psi p_0\\ \psi p_1 \\ \psi p_2 \\ \psi p_3 \\ \vdots \end{bmatrix} \\ &\iff& \begin{cases} p_1 &= \psi p_0 \\ p_2 &= \frac{\psi}{2} p_1 \\ p_3 &= \frac{\psi}{3} p_2 \\ &\dots \end{cases} & \end{align*}\]This system of equations implies that all coefficients are determined solely by our choice of constants \(p_0\) and \(\psi\). We can explicitly write down their relationship as \(p_i = \frac{\psi^i}{i!}p_0\).
Now, let’s see what this class of polynomials actually looks like.
Differentiation shows that this function is, in fact, an eigenfunction for the eigenvalue \(\psi\).
With a bit of algebraic manipulation, the definition of \(e^{x}\) pops out:
Therefore, functions of the form \(p_0e^{\psi x}\) are eigenfunctions for the eigenvalue \(\psi\), including when \(\psi=0\).
We’ve found the eigenfunctions of the derivative operator, but can we diagonalize it? Ideally, we would express differentiation as the combination of an invertible operator \(\mathcal{L}\) and a diagonal operator \(\mathcal{D}\).
Diagonalization is only possible when our eigenfunctions form a basis. This would be true if all analytic functions are expressible as a linear combination of exponentials. However…
First assume that \(f[x] = x\) can be represented as a linear combination of exponentials. Since analytic functions have countably infinite dimensionality, we should only need a countably infinite sum:
\[f[x] = x = \sum_{n=0}^\infty \alpha_n e^{\psi_n x}\]Differentiating both sides:
\[\begin{align*} f^{\prime}[x] &= 1 = \sum_{n=0}^\infty \psi_n\alpha_n e^{\psi_n x} \\ f^{\prime\prime}[x] &= 0 = \sum_{n=0}^\infty \psi_n^2\alpha_n e^{\psi_n x} \end{align*}\]Since \(e^{\psi_n x}\) and \(e^{\psi_m x}\) are linearly independent when \(n\neq m\), the final equation implies that all \(\alpha = 0\), except possibly the \(\alpha_\xi\) corresponding to \(\psi_\xi = 0\). Therefore:
\[\begin{align*} 1 &= \sum_{n=0}^\infty \psi_n\alpha_n e^{\psi_n x}\\ &= \psi_\xi \alpha_\xi + \sum_{n\neq \xi} 0\psi_n e^{\psi_n x} \\ &= 0 \end{align*}\]That’s a contradiction—the linear combination representing \(f[x] = x\) does not exist.
A similar argument shows that we can’t represent any non-constant function whose \(n\)th derivative is zero, nor periodic functions like sine and cosine.
Real exponentials don’t constitute a basis, so we cannot construct an invertible \(\mathcal{L}\).
We previously mentioned that more matrices can be diagonalized if we allow the decomposition to contain complex numbers. Analogously, more linear operators are diagonalizable in the larger vector space of functions from \(\mathbb{R}\) to \(\mathbb{C}\).
Differentiation works the same way in this space; we’ll still find that its eigenfunctions are exponential.
\[\frac{\partial}{\partial x} e^{(a+bi)x} = (a+bi)e^{(a+bi)x}\]However, the new eigenfunctions have complex eigenvalues, so we still can’t diagonalize. We’ll need to consider the still larger space of functions from \(\mathbb{C}\) to \(\mathbb{C}\).
\[\frac{\partial}{\partial x} : (\mathbb{C}\mapsto\mathbb{C}) \mapsto (\mathbb{C}\mapsto\mathbb{C})\]In this space, differentiation can be diagonalized via the Laplace transform. Although useful for solving differential equations, the Laplace transform is non-trivial to invert, so we won’t discuss it further. In the following sections, we’ll delve into an operator that can be easily diagonalized in \(\mathbb{R}\mapsto\mathbb{C}\): the Laplacian.
Before we get to the spectral theorem, we’ll need to understand one more topic: inner products. You’re likely already familiar with one example of an inner product—the Euclidean dot product.
\[\begin{bmatrix}x\\ y\\ z\end{bmatrix} \cdot \begin{bmatrix}a\\ b\\ c\end{bmatrix} = ax + by + cz\]An inner product describes how to measure a vector along another vector. For example, \(\mathbf{u}\cdot\mathbf{v}\) is proportional to the length of the projection of \(\mathbf{u}\) onto \(\mathbf{v}\).
With a bit of trigonometry, we can show that the dot product is equivalent to multiplying the vectors’ lengths with the cosine of their angle. This relationship suggests that the product of a vector with itself produces the square of its length.
\[\begin{align*} \mathbf{u}\cdot\mathbf{u} &= \|\mathbf{u}\|\|\mathbf{u}\|\cos[0] \\ &= \|\mathbf{u}\|^2 \end{align*}\]Similarly, when two vectors form a right angle (are orthogonal), their dot product is zero.
Of course, the Euclidean dot product is only one example of an inner product. In more general spaces, the inner product is denoted using angle brackets, such as \(\langle \mathbf{u}, \mathbf{v} \rangle\).
A vector space augmented with an inner product is known as an inner product space.
We can’t directly apply the Euclidean dot product to our space of real functions, but its \(N\)-dimensional generalization is suggestive.
\[\begin{align*} \mathbf{u} \cdot \mathbf{v} &= u_1v_1 + u_2v_2 + \dots + u_Nv_N \\ &= \sum_{i=1}^N u_iv_i \end{align*}\]Given countable indices, we simply match up the values, multiply them, and add the results. When indices are uncountable, we can convert the discrete sum to its continuous analog: an integral!
\[\langle f, g \rangle = \int_a^b f[x]g[x] \, dx\]When \(f\) and \(g\) are similar, multiplying them produces a larger function; when they’re different, they cancel out. Integration measures their product over some domain to produce a scalar result.
Of course, not all functions can be integrated. Our inner product space will only contain functions that are square integrable over the domain \([a, b]\), which may be \([-\infty, \infty]\). Luckily, the important properties of our inner product do not depend on the choice of integration domain.
Below, we’ll briefly cover functions from \(\mathbb{R}\) to \(\mathbb{C}\). In this space, our intuitive notion of similarity still applies, but we’ll use a slightly more general inner product:
\[\langle f,g \rangle = \int_a^b f[x]\overline{g[x]}\, dx\]Where \(\overline{x}\) denotes conjugation, i.e. \(\overline{a + bi} = a - bi\).
Like other vector space operations, an inner product must satisfy several axioms:
Along with the definition \(\|f\| = \sqrt{\langle f, f \rangle}\), these properties entail a variety of important results, including the Cauchy–Schwarz and triangle inequalities.
Diagonalization is already a powerful technique, but we’re building up to an even more important result regarding orthonormal eigenbases. In an inner product space, an orthonormal basis must satisfy two conditions: each vector is unit length, and all vectors are mutually orthogonal.
A matrix consisting of orthonormal columns is known as an orthogonal matrix. Orthogonal matrices represent rotations of the standard basis.
In an inner product space, matrix-vector multiplication computes the inner product of the vector with each row of the matrix. Something interesting happens when we multiply an orthogonal matrix \(\mathbf{U}\) by its transpose:
Since \(\mathbf{U}^T\mathbf{U} = \mathcal{I}\) (and \(\mathbf{U}\mathbf{U}^T = \mathcal{I}\)), we’ve found that the transpose of \(\mathbf{U}\) is equal to its inverse.
When diagonalizing \(\mathbf{A}\), we used \(\mathbf{U}\) to transform vectors from our eigenbasis to the standard basis. Conversely, its inverse transformed vectors from the standard basis to our eigenbasis. If \(\mathbf{U}\) happens to be orthogonal, transforming a vector \(\mathbf{x}\) into the eigenbasis is equivalent to projecting \(\mathbf{x}\) onto each eigenvector.
Additionally, the diagonalization of \(\mathbf{A}\) becomes quite simple:
Given an orthogonal diagonalization of \(\mathbf{A}\), we can deduce that \(\mathbf{A}\) must be symmetric, i.e. \(\mathbf{A} = \mathbf{A}^T\).
\[\begin{align*} \mathbf{A}^T &= (\mathbf{U\Lambda U}^T)^T \\ &= {\mathbf{U}^T}^T \mathbf{\Lambda }^T \mathbf{U}^T \\ &= \mathbf{U\Lambda U}^T \\ &= \mathbf{A} \end{align*}\]The spectral theorem states that the converse is also true: \(\mathbf{A}\) is symmetric if and only if it admits an orthonormal eigenbasis with real eigenvalues. Proving this result is somewhat involved in finite dimensions and very involved in infinite dimensions, so we won’t reproduce the proofs here.
We can generalize the spectral theorem to our space of functions, where it states that a self-adjoint operator admits an orthonormal eigenbasis with real eigenvalues.6
Denoted as \(\mathbf{A}^{\hspace{-0.1em}\star\hspace{0.1em}}\), the adjoint of an operator \(\mathbf{A}\) is defined by the following relationship.
\[\langle \mathbf{Ax}, \mathbf{y} \rangle = \langle \mathbf{x}, \mathbf{A}^{\hspace{-0.1em}\star\hspace{0.1em}}\mathbf{y} \rangle\]When \(\mathbf{A} = \mathbf{A}^\star\), we say that \(\mathbf{A}\) is self-adjoint.
The adjoint can be thought of as a generalized transpose—but it’s not obvious what that means in infinite dimensions. We will simply use our functional inner product to determine whether an operator is self-adjoint.
Review: Solving the heat equation | DE3.
Earlier, we weren’t able to diagonalize (real) differentiation, so it must not be self-adjoint. Therefore, we will explore another fundamental operator, the Laplacian.
There are many equivalent definitions of the Laplacian, but in our space of one-dimensional functions, it’s just the second derivative. We will hence restrict our domain to twice-differentiable functions.
\[\Delta f = \frac{\partial^2 f}{\partial x^2}\]We may compute \(\Delta^\star\) using two integrations by parts:
In the final step, we assume that \((f^\prime[x]g[x] - f[x]g^{\prime}[x])\big|_a^b = 0\), which is not true in general. To make our conclusion valid, we will constrain our domain to only include functions satisfying this boundary condition. Specifically, we will only consider periodic functions with period \(b-a\). These functions have the same value and derivative at \(a\) and \(b\), so the additional term vanishes.
For simplicity, we will also assume our domain to be \([0,1]\). For example:
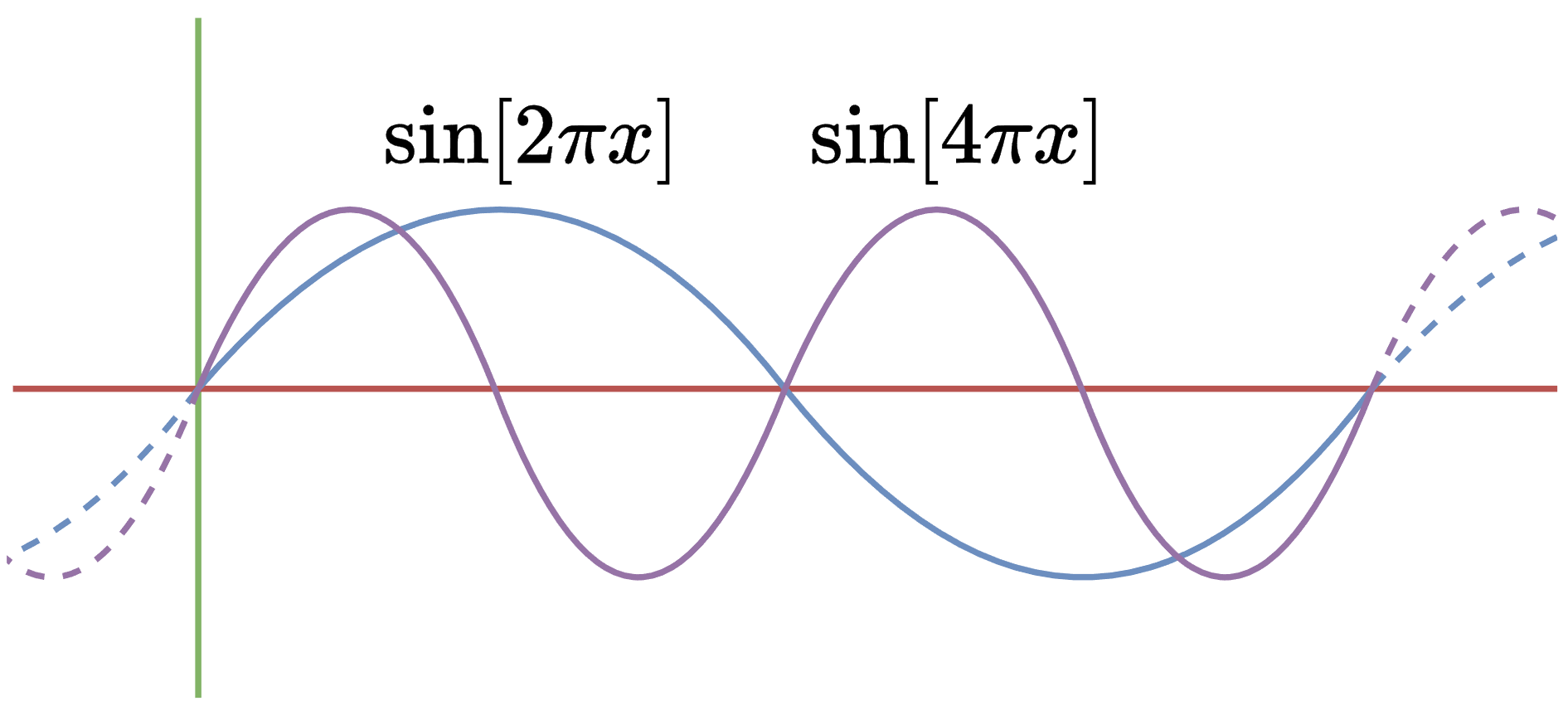
Therefore, the Laplacian is self-adjoint…almost. Technically, we’ve shown that the Laplacian is symmetric, not that \(\Delta = \Delta^\star\). This is a subtle point, and it’s possible to prove self-adjointness, so we will omit this detail.
Applying the spectral theorem tells us that the Laplacian admits an orthonormal eigenbasis. Let’s find it.7
Since the Laplacian is simply the second derivative, real exponentials would still be eigenfunctions—but they’re not periodic, so we’ll have to exclude them.
\[\color{red} \Delta e^{\psi x} = \psi^2 e^{\psi x}\]Luckily, a new class of periodic eigenfunctions appears:
\[\begin{align*} \Delta \sin[\psi x] &= -\psi^2 \sin[\psi x] \\ \Delta \cos[\psi x] &= -\psi^2 \cos[\psi x] \end{align*}\]If we allow our diagonalization to introduce complex numbers, we can also consider functions from \(\mathbb{R}\) to \(\mathbb{C}\) . Here, purely complex exponentials are eigenfunctions with real eigenvalues.
Using Euler’s formula, we can see that these two perspectives are equivalent: they both introduce \(\sin\) and \(\cos\) as eigenfunctions. Either path can lead to our final result, but we’ll stick with the more compact complex case.
We also need to constrain the set of eigenfunctions to be periodic on \([0,1]\). As suggested above, we can pick out the eigenvalues that are an integer multiple of \(2\pi\).
\[e^{2\pi \xi i x} = \cos[2\pi \xi x] + i\sin[2\pi \xi x]\]Our set of eigenfunctions is therefore \(e^{2\pi \xi i x}\) for all integers \(\xi\).
Now that we’ve found suitable eigenfunctions, we can construct an orthonormal basis.
Our collection of eigenfunctions is linearly independent, as each one corresponds to a distinct eigenvalue. Next, we can check for orthogonality and unit magnitude:
Compute the inner product of \(e^{2\pi \xi_1 i x}\) and \(e^{2\pi \xi_2 i x}\) for \(\xi_1 \neq \xi_2\):
Note that the final step is valid because \(\xi_1-\xi_2\) is a non-zero integer.
This result also applies to any domain \([a,b]\), given functions periodic on \([a,b]\).
It’s possible to further generalize to \([-\infty,\infty]\), but doing so requires a weighted inner product.
It’s easy to show that all candidate functions have norm one:
\[\begin{align*} \langle e^{2\pi\xi i x}, e^{2\pi\xi i x} \rangle &= \int_0^1 e^{2\pi\xi i x}\overline{e^{2\pi\xi i x}} \\ &= \int_0^1 e^{2\pi\xi i x}e^{-2\pi\xi i x}\, dx \\&= \int_0^1 1\, dx\\ &= 1 \end{align*}\]With the addition of a constant factor \(\frac{1}{b-a}\), this result generalizes to any \([a,b]\).
It’s possible to further generalize to \([-\infty,\infty]\), but doing so requires a weighted inner product.
The final step is to show that all functions in our domain can be represented by a linear combination of eigenfunctions. To do so, we will find an invertible operator \(\mathcal{L}\) representing the proper change of basis.
Critically, since our eigenbasis is orthonormal, we can intuitively consider the inverse of \(\mathcal{L}\) to be its transpose.
This visualization suggests that \(\mathcal{L}^Tf\) computes the inner product of \(f\) with each eigenvector.
\[\mathcal{L}^Tf = \begin{bmatrix}\langle f, e^{2\pi\xi_1 i x} \rangle \\ \langle f, e^{2\pi\xi_2 i x} \rangle \\ \vdots \end{bmatrix}\]Which is highly reminiscent of the finite-dimensional case, where we projected onto each eigenvector of an orthogonal eigenbasis.
This insight allows us to write down the product \(\mathcal{L}^Tf\) as an integer function \(\hat{f}[\xi]\). Note that the complex inner product conjugates the second argument, so the exponent is negated.
\[(\mathcal{L}^Tf)[\xi] = \hat{f}[\xi] = \int_0^1 f[x]e^{-2\pi\xi i x}\, dx\]Conversely, \(\mathcal{L}\) converts \(\hat{f}\) back to the standard basis. It simply creates a linear combination of eigenfunctions.
\[(\mathcal{L}\hat{f})[x] = f[x] = \sum_{\xi=-\infty}^\infty \hat{f}[\xi] e^{2\pi\xi i x}\]These operators are, in fact, inverses of each other, but a rigorous proof is beyond the scope of this post. Therefore, we’ve diagonalized the Laplacian:
Although \(\mathcal{L}^T\) transforms our real-valued function into a complex-valued function, \(\Delta\) as a whole still maps real functions to real functions. Next, we’ll see how \(\mathcal{L}^T\) is itself an incredibly useful transformation.
In this section, we’ll explore several applications in signal processing, each of which arises from diagonalizing the Laplacian on a new domain.
If you’re familiar with Fourier methods, you likely noticed that \(\hat{f}\) encodes the Fourier series of \(f\). That’s because a Fourier transform is a change of basis into the Laplacian eigenbasis!
This basis consists of waves, which makes \(\hat{f}\) a particularly interesting representation for \(f\). For example, consider evaluating \(\hat{f}[1]\):
This integral measures how much of \(f\) is represented by waves of frequency (positive) 1. Naturally, \(\hat{f}[\xi]\) computes the same quantity for any integer frequency \(\xi\).
\[\hphantom{aaa} {\color{#9673A6} \text{Real}\left[e^{2\pi i \xi x}\right]}\,\,\,\,\,\,\,\, {\color{#D79B00} \text{Complex}\left[e^{2\pi i \xi x}\right]}\]$$\xi = 1$$
Therefore, we say that \(\hat{f}\) expresses our function in the frequency domain. To illustrate this point, we’ll use a Fourier series to decompose a piecewise linear function into a collection of waves.8 Since our new basis is orthonormal, the transform is easy to invert by re-combining the waves.
Here, the \(\color{#9673A6}\text{purple}\) curve is \(f\); the \(\color{#D79B00}\text{orange}\) curve is a reconstruction of \(f\) from the first \(N\) coefficients of \(\hat{f}\). Try varying the number of coefficients and moving the \(\color{#9673A6}\text{purple}\) dots to effect the results.
$$N = 3$$
| $$\hat{f}[0]$$ | $$\hat{f}[1]e^{2\pi i x}$$ | $$\hat{f}[2]e^{4\pi i x}$$ | $$\hat{f}[3]e^{6\pi i x}$$ |
Many interesting operations become easy to compute in the frequency domain. For example, by simply dropping Fourier coefficients beyond a certain threshold, we can reconstruct a smoothed version of our function. This technique is known as a low-pass filter—try it out above.
Computationally, Fourier series are especially useful for compression. Encoding a function \(f\) in the standard basis takes a lot of space, since we store a separate result for each input. If we instead express \(f\) in the Fourier basis, we only need to store a few coefficients—we’ll be able to approximately reconstruct \(f\) by re-combining the corresponding basis functions.
So far, we’ve only defined a Fourier transform for functions on \(\mathbb{R}\). Luckily, the transform arose via diagonalizing the Laplacian, and the Laplacian is not limited to one-dimensional functions. In fact, wherever we can define a Laplacian, we can find a corresponding Fourier transform.9
For example, in two dimensions, the Laplacian becomes a sum of second derivatives.
\[\Delta f[x,y] = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}\]For the domain \([0,1]\times[0,1]\), we’ll find a familiar set of periodic eigenfunctions.
Where \(n\) and \(m\) are both integers. Let’s see what these basis functions look like:
$$n = 3$$
$$m = 3$$
Just like the 1D case, the corresponding Fourier transform is a change of basis into the Laplacian’s orthonormal eigenbasis. Above, we decomposed a 1D function into a collection of 1D waves—here, we equivalently decompose a 2D image into a collection of 2D waves.
$$N = 3$$
A variant of the 2D Fourier transform is at the core of many image compression algorithms, including JPEG.
Computer graphics is often concerned with functions on the unit sphere, so let’s see if we can find a corresponding Fourier transform. In spherical coordinates, the Laplacian can be defined as follows:
We won’t go through the full derivation, but this Laplacian admits an orthornormal eigenbasis known as the spherical harmonics.10
\[Y_\ell^m[\theta, \phi] = N_\ell^m P_\ell^m[\cos[\theta]] e^{im\phi}\]Where \(Y_\ell^m\) is the spherical harmonic of degree \(\ell \ge 0\) and order \(m \in [-\ell,\ell]\). Note that \(N_\ell^m\) is a constant and \(P_\ell^m\) are the associated Legendre polynomials.11
\[\hphantom{aa} {\color{#9673A6} \text{Real}\left[Y_\ell^m[\theta,\phi]\right]}\,\,\,\,\,\,\,\, {\color{#D79B00} \text{Complex}\left[Y_\ell^m[\theta,\phi]\right]}\]$$\ell = 0$$
$$m = 0$$
As above, we define the spherical Fourier transform as a change of basis into the spherical harmonics. In game engines, this transform is often used to compress diffuse environment maps (i.e. spherical images) and global illumination probes.
$$N = 3$$
You might also recognize spherical harmonics as electron orbitals—quantum mechanics is primarily concerned with the eigenfunctions of linear operators.
Representing functions as vectors underlies many modern algorithms—image compression is only one example. In fact, because computers can do linear algebra so efficiently, applying linear-algebraic techniques to functions produces a powerful new computational paradigm.
The nascent field of discrete differential geometry uses this perspective to build algorithms for three-dimensional geometry processing. In computer graphics, functions on meshes often represent textures, unwrappings, displacements, or simulation parameters. DDG gives us a way to faithfully encode such functions as vectors: for example, by associating a value with each vertex of the mesh.
One particularly relevant result is a Laplace operator for meshes. A mesh Laplacian is a finite-dimensional matrix, so we can use numerical linear algebra to find its eigenfunctions.
As with the continuous case, these functions generalize sine and cosine to a new domain. Here, we visualize the real and complex parts of each eigenfunction, where the two colors indicate positive vs. negative regions.
\[\hphantom{aa} {\color{#9673A6} \text{Rea}}{\color{#82B366}\text{l}\left[\psi_N\right]}\,\,\,\,\,\,\,\, {\color{#D79B00} \text{Comp}}{\color{#6C8EBF} \text{lex}\left[\psi_N\right]}\]$$4\text{th Eigenfunction}$$
At this point, the implications might be obvious—this eigenbasis is useful for transforming and compressing functions on the mesh. In fact, by interpreting the vertices’ positions as a function, we can even smooth or sharpen the geometry itself.
There’s far more to signal and geometry processing than we can cover here, let alone the many other applications in engineering, physics, and computer science. We will conclude with an (incomplete, biased) list of topics for further exploration. See if you can follow the functions-are-vectors thread throughout:
Thanks to Joanna Y, Hesper Yin, and Fan Pu Zeng for providing feedback on this post.
We shouldn’t assume all countably infinite-dimensional vectors represent functions on the natural numbers. Later on, we’ll discuss the space of real polynomial functions, which also has countably infinite dimensionality. ↩
If you’re alarmed by the fact that the set of all real functions does not form a Hilbert space, you’re probably not in the target audience of this post. Don’t worry, we will later move on to \(L^2(\mathbb{R})\) and \(L^2(\mathbb{R},\mathbb{C})\). ↩
If you’re paying close attention, you might notice that none of these proofs depended on the fact that the domain of our functions is the real numbers. In fact, the only necessary assumption is that our functions return elements of a field, allowing us to apply commutativity, associativity, etc. to the outputs.
Therefore, we can define a vector space over the set of functions that map any fixed set \(\mathcal{S}\) to a field \(\mathbb{F}\). This result illustrates why we could intuitively equate finite-dimensional vectors with mappings from index to value. For example, consider \(\mathcal{S} = \{1,2,3\}\):
If \(\mathcal{S}\) is finite, a function from \(\mathcal{S}\) to a field directly corresponds to a familiar finite-dimensional vector. ↩
Earlier, we used countably infinite-dimensional vectors to represent functions on the natural numbers. In doing so, we implicitly employed the standard basis of impulse functions indexed by \(i \in \mathbb{N}\). Here, we encode real polynomials by choosing new basis functions of type \(\mathbb{R}\mapsto\mathbb{R}\), namely \(\mathbf{e}_i[x] = x^i\). ↩
Since this basis spans the space of analytic functions, analytic functions have countably infinite dimensionality. Relative to the uncountably infinite-dimensional space of all real functions, analytic functions are vanishingly rare! ↩
Actually, it states that a compact self-adjoint operator on a Hilbert space admits an orthonormal eigenbasis with real eigenvalues. Rigorously defining these terms is beyond the scope of this post, but note that our intuition about “infinite-dimensional matrices” only legitimately applies to this class of operators. ↩
Specifically, a basis for the domain of our Laplacian, not all functions. We’ve built up several conditions that restrict our domain to square integrable, periodic, twice-differentiable real functions on \([0,1]\). ↩
Also known as a vibe check. ↩
Higher-dimensional Laplacians are sums of second derivatives, e.g. \(\Delta f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2} + \frac{\partial^2 f}{\partial z^2}\). The Laplace-Beltrami operator expresses this sum as the divergence of the gradient, i.e. \(\Delta f = \nabla \cdot \nabla f\). Using exterior calculus, we can further generalize divergence and gradient to produce the Laplace-de Rham operator, \(\Delta f = \delta d f\), where \(\delta\) is the codifferential and \(d\) is the exterior derivative. ↩
Typically, a “harmonic” function must satisfy \(\Delta f = 0\), but in this case we include all eigenfunctions. ↩
The associated Legendre polynomials are closely related to the Legendre polynomials, which form a orthogonal basis for polynomials. Interestingly, they can be derived by applying the Gram–Schmidt process to the basis of powers (\(1, x, x^2, \dots\)). ↩




























Code for this article may be found on GitHub.
Most people first encounter hash tables implemented using separate chaining, a model simple to understand and analyze mathematically. In separate chaining, a hash function is used to map each key to one of \(K\) buckets. Each bucket holds a linked list, so to retrieve a key, one simply traverses its corresponding bucket.
Given a hash function drawn from a universal family, inserting \(N\) keys into a table with \(K\) buckets results in an expected bucket size of \(\frac{N}{K}\), a quantity also known as the table’s load factor. Assuming (reasonably) that \(\frac{N}{K}\) is bounded by a constant, all operations on such a table can be performed in expected constant time.
Unfortunately, this basic analysis doesn’t consider the myriad factors that go into implementing an efficient hash table on a real computer. In practice, hash tables based on open addressing can provide superior performance, and their limitations can be worked around in nearly all cases.
In an open-addressed table, each bucket only contains a single key. Collisions are handled by placing additional keys elsewhere in the table. For example, in linear probing, a key is placed in the first open bucket starting from the index it hashes to.
Unlike in separate chaining, open-addressed tables may be represented in memory as a single flat array. A priori, we should expect operations on flat arrays to offer higher performance than those on linked structures due to more coherent memory accesses.1
However, if the user wants to insert more than \(K\) keys into an open-addressed table with \(K\) buckets, the entire table must be resized. Typically, a larger array is allocated and all current keys are moved to the new table. The size is grown by a constant factor (e.g. 2x), so insertions occur in amortized constant time.
In practice, the standard libraries of many languages provide separately chained hash tables, such as C++’s std::unordered_map.
At least in C++, this choice is now considered to have been a mistake—it violates C++’s principle of not paying for features you didn’t ask for.
Separate chaining still has some purported benefits, but they seem unconvincing:
Separately chained tables don’t require any linear-time operations.
First, this isn’t true.
To maintain a constant load factor, separate chaining hash tables also have to resize once a sufficient number of keys are inserted, though the limit can be greater than \(K\).
Most separately chained tables, including std::unordered_map, only provide amortized constant time insertion.
Second, open-addressed tables can be incrementally resized. When the table grows, there’s no reason we have to move all existing keys right away. Instead, every subsequent operation can move a fixed number of old keys into the new table. Eventually, all keys will have been moved and the old table may be deallocated. This technique incurs overhead on every operation during a resize, but none will require linear time.
When each (key + value) entry is allocated separately, entries can have stable addresses. External code can safely store pointers to them, and large entries never have to be copied.
This property is easy to support by adding a single level of indirection. That is, allocate each entry separately, but use an open-addressed table to map keys to pointers-to-entries. In this case, resizing the table only requires copying pointers, rather than entire entries.
Lower memory overhead.
It’s possible for a separately chained table to store the same data in less space than an open-addressed equivalent, since flat tables necessarily waste space storing empty buckets. However, matching high-quality open addressing schemes (especially when storing entries indirectly) requires a load factor greater than one, degrading query performance. Further, individually allocating nodes wastes memory due to heap allocator overhead and fragmentation.
In fact, the only situation where open addressing truly doesn’t work is when the table cannot allocate and entries cannot be moved. These requirements can arise when using intrusive linked lists, a common pattern in kernel data structures and embedded systems with no heap.
For simplicity, let us only consider tables mapping 64-bit integer keys to 64-bit integer values. Results will not take into account the effects of larger values or non-trivial key comparison, but should still be representative, as keys can often be represented in 64 bits and values are often pointers.
We will evaluate tables using the following metrics:
Each open-addressed table was benchmarked at 50%, 75%, and 90% load factors. Every test targeted a table capacity of 8M entries, setting \(N = \lfloor 8388608 * \text{Load Factor} \rfloor - 1\). Fixing the table capacity allows us to benchmark behavior at exactly the specified load factor, avoiding misleading results from tables that have recently grown. The large number of keys causes each test to unpredictably traverse a data set much larger than L3 cache (128MB+), so the CPU3 cannot effectively cache or prefetch memory accesses.
All benchmarked tables use exclusively power-of-two sizes. This invariant allows us to translate hashes to array indices with a fast bitwise AND operation, since:
h % 2**n == h & (2**n - 1)
Power-of-two sizes also admit a neat virtual memory trick,4 but that optimization is not included here.
However, power-of-two sizes can cause pathological behavior when paired with some hash functions, since indexing simply throws away the hash’s high bits. An alternative strategy is to use prime sized tables, which are significantly more robust to the choice of hash function. For the purposes of this post, we have a fixed hash function and non-adversarial inputs, so prime sizes were not used.5
All benchmarked tables use the squirrel3 hash function, a fast integer hash that (as far as I can tell) only exists in this GDC talk on noise-based RNG.
Here, it is adapted to 64-bit integers by choosing three large 64-bit primes:
uint64_t squirrel3(uint64_t at) {
constexpr uint64_t BIT_NOISE1 = 0x9E3779B185EBCA87ULL;
constexpr uint64_t BIT_NOISE2 = 0xC2B2AE3D27D4EB4FULL;
constexpr uint64_t BIT_NOISE3 = 0x27D4EB2F165667C5ULL;
at *= BIT_NOISE1;
at ^= (at >> 8);
at += BIT_NOISE2;
at ^= (at << 8);
at *= BIT_NOISE3;
at ^= (at >> 8);
return at;
}
I make no claims regarding the quality or robustness of this hash function, but observe that it’s cheap, it produces the expected number of collisions in power-of-two tables, and it passes smhasher when applied bytewise.
Several less interesting benchmarks were also run, all of which exhibited identical performance across equal-memory open-addressed tables and much worse performance for separate chaining.
To get our bearings, let’s first implement a simple separate chaining table and benchmark it at various load factors.
| Separate Chaining | 50% Load | 100% Load | 200% Load | 500% Load | ||||
| Existing | Missing | Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 115 | 113 | 120 | 152 | ||||
| Erase (ns/key) | 110 | 128 | 171 | 306 | ||||
| Lookup (ns/key) | 28 | 28 | 35 | 40 | 50 | 68 | 102 | 185 |
| Average Probe | 1.25 | 0.50 | 1.50 | 1.00 | 2.00 | 2.00 | 3.50 | 5.00 |
| Max Probe | 7 | 7 | 10 | 9 | 12 | 13 | 21 | 21 |
| Memory Amplification | 2.50 | 2.00 | 1.75 | 1.60 | ||||
These are respectable results, especially lookups at 100%: the CPU is able to hide much of the memory latency. Insertions and erasures, on the other hand, are pretty slow—they involve allocation.
Technically, the reported memory amplification in an underestimate, as it does not include heap allocator overhead. However, we should not directly compare memory amplification against the coming open-addressed tables, as storing larger values would improve separate chaining’s ratio.
std::unordered_mapRunning these benchmarks on std::unordered_map<uint64_t,uint64_t> produces results roughly equivalent to the 100% column, just with marginally slower insertions and faster clears.
Using squirrel3 with std::unordered_map additionally makes insertions slightly slower and lookups slightly faster.
Further comparisons will be relative to these results, since exact performance numbers for std::unordered_map depend on one’s standard library distribution (here, Microsoft’s).
Next, let’s implement the simplest type of open addressing—linear probing.
In the following diagrams, assume that each letter hashes to its alphabetical index. The skull denotes a tombstone.
Insert: starting from the key’s index, place the key in the first empty or tombstone bucket.
Lookup: starting from the key’s index, probe buckets in order until finding the key, reaching an empty non-tombstone bucket, or exhausting the table.
Erase: lookup the key and replace it with a tombstone.
The results are surprisingly good, considering the simplicity:
| Linear Probing (Naive) | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 46 | 59 | 73 | |||
| Erase (ns/key) | 21 | 36 | 47 | |||
| Lookup (ns/key) | 20 | 86 | 35 | 124 | 47 | 285 |
| Average Probe | 0.50 | 6.04 | 1.49 | 29.5 | 4.46 | 222 |
| Max Probe | 43 | 85 | 181 | 438 | 1604 | 2816 |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
For existing keys, we’re already beating the separately chained tables, and with lower memory overhead! Of course, there are also some obvious problems—looking for missing keys takes much longer, and the worst-case probe lengths are quite scary, even at 50% load factor. But, we can do much better.
One simple optimization is automatically recreating the table once it accumulates too many tombstones. Erase now occurs in amortized constant time, but we already tolerate that for insertion, so it shouldn’t be a big deal. Let’s implement a table that re-creates itself after erase has been called \(\frac{N}{2}\) times.
Compared to naive linear probing:
| Linear Probing + Rehashing | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 46 | 58 | 70 | |||
| Erase (ns/key) | 23 (+10.4%) | 27 (-23.9%) | 29 (-39.3%) | |||
| Lookup (ns/key) | 20 | 85 | 35 | 93 (-25.4%) | 46 | 144 (-49.4%) |
| Average Probe | 0.50 | 6.04 | 1.49 | 9.34 (-68.3%) | 4.46 | 57.84 (-74.0%) |
| Max Probe | 43 | 85 | 181 | 245 (-44.1%) | 1604 | 1405 (-50.1%) |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
Clearing the tombstones dramatically improves missing key queries, but they are still pretty slow. It also makes erase slower at 50% load—there aren’t enough tombstones to make up for having to recreate the table. Rehashing also does nothing to mitigate long probe sequences for existing keys.
Actually, who says we need tombstones? There’s a little-taught, but very simple algorithm for erasing keys that doesn’t degrade performance or have to recreate the table.
When we erase a key, we don’t know whether the lookup algorithm is relying on our bucket being filled to find keys later in the table. Tombstones are one way to avoid this problem. Instead, however, we can guarantee that traversal is never disrupted by simply removing and reinserting all following keys, up to the next empty bucket.
Note that despite the name, we are not simply shifting the following keys backward. Any keys that are already at their optimal index will not be moved. For example:
After implementing backward-shift deletion, we can compare it to linear probing with rehashing:
| Linear Probing + Backshift | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 46 | 58 | 70 | |||
| Erase (ns/key) | 47 (+105%) | 82 (+201%) | 147 (+415%) | |||
| Lookup (ns/key) | 20 | 37 (-56.2%) | 36 | 88 | 46 | 135 |
| Average Probe | 0.50 | 1.50 (-75.2%) | 1.49 | 7.46 (-20.1%) | 4.46 | 49.7 (-14.1%) |
| Max Probe | 43 | 50 (-41.2%) | 181 | 243 | 1604 | 1403 |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
Naturally, erasures become significantly slower, but queries on missing keys now have reasonable behavior, especially at 50% load. In fact, at 50% load, this table already beats the performance of equal-memory separate chaining in all four metrics. But, we can still do better: a 50% load factor is unimpressive, and max probe lengths are still very high compared to separate chaining.
You might have noticed that neither of these upgrades improved average probe length for existing keys. That’s because it’s not possible for linear probing to have any other average! Think about why that is—it’ll be interesting later.
Quadratic probing is a common upgrade to linear probing intended to decrease average and maximum probe lengths.
In the linear case, a probe of length \(n\) simply queries the bucket at index \(h(k) + n\). Quadratic probing instead queries the bucket at index \(h(k) + \frac{n(n+1)}{2}\). Other quadratic sequences are possible, but this one can be efficiently computed by adding \(n\) to the index at each step.
Each operation must be updated to use our new probe sequence, but the logic is otherwise almost identical:
There are a couple subtle caveats to quadratic probing:
After implementing our quadratic table, we can compare it to linear probing with rehashing:
| Quadratic Probing + Rehashing | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 47 | 54 (-7.2%) | 65 (-6.4%) | |||
| Erase (ns/key) | 23 | 28 | 29 | |||
| Lookup (ns/key) | 20 | 82 | 31 (-13.2%) | 93 | 42 (-7.3%) |
163 (+12.8%) |
| Average Probe | 0.43 (-12.9%) | 4.81 (-20.3%) | 0.99 (-33.4%) | 5.31 (-43.1%) | 1.87 (-58.1%) | 18.22 (-68.5%) |
| Max Probe | 21 (-51.2%) | 49 (-42.4%) | 46 (-74.6%) | 76 (-69.0%) | 108 (-93.3%) | 263 (-81.3%) |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
As expected, quadratic probing dramatically reduces both the average and worst case probe lengths, especially at high load factors. These gains are not quite as impressive when compared to the linear table with backshift deletion, but are still very significant.
Reducing the average probe length improves the average performance of all queries. Erasures are the fastest yet, since quadratic probing quickly finds the element and marks it as a tombstone. However, beyond 50% load, maximum probe lengths are still pretty concerning.
Double hashing purports to provide even better behavior than quadratic probing. Instead of using the same probe sequence for every key, double hashing determines the probe stride by hashing the key a second time. That is, a probe of length \(n\) queries the bucket at index \(h_1(k) + n*h_2(k)\)
So far, we’ve been throwing away the high bits our of 64-bit hash when computing table indices. Instead of evaluating a second hash function, let’s just re-use the top 32 bits: \(h_2(k) = h_1(k) >> 32\).
After implementing double hashing, we may compare the results to quadratic probing with rehashing:
| Double Hashing + Rehashing | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 70 (+49.6%) | 80 (+48.6%) | 88 (+35.1%) | |||
| Erase (ns/key) | 31 (+33.0%) | 43 (+53.1%) | 47 (+61.5%) | |||
| Lookup (ns/key) | 29 (+46.0%) | 84 | 38 (+25.5%) | 93 | 49 (+14.9%) | 174 |
| Average Probe | 0.39 (-11.0%) | 4.39 (-8.8%) | 0.85 (-14.7%) | 4.72 (-11.1%) | 1.56 (-16.8%) | 16.23 (-10.9%) |
| Max Probe | 17 (-19.0%) | 61 (+24.5%) | 44 (-4.3%) |
83 (+9.2%) |
114 (+5.6%) | 250 (-4.9%) |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
Double hashing succeeds in further reducing average probe lengths, but max lengths are more of a mixed bag. Unfortunately, most queries now traverse larger spans of memory, causing performance to lag quadratic hashing.
So far, quadratic probing and double hashing have provided lower probe lengths, but their raw performance isn’t much better than linear probing—especially on missing keys. Enter Robin Hood linear probing. This strategy drastically reins in maximum probe lengths while maintaining high query performance.
The key difference is that when inserting a key, we are allowed to steal the position of an existing key if it is closer to its ideal index (“richer”) than the new key is. When this occurs, we simply swap the old and new keys and carry on inserting the old key in the same manner. This results in a more equitable distribution of probe lengths.
This insertion method turns out to be so effective that we can entirely ignore rehashing as long as we keep track of the maximum probe length. Lookups will simply probe until either finding the key or exhausting the maximum probe length.
Implementing this table, compared to linear probing with backshift deletion:
| Robin Hood (Naive) | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 53 (+16.1%) | 80 (+38.3%) | 124 (+76.3%) | |||
| Erase (ns/key) | 19 (-58.8%) | 31 (-63.0%) | 77 (-47.9%) | |||
| Lookup (ns/key) | 19 | 58 (+56.7%) | 31 (-11.3%) | 109 (+23.7%) | 79 (+72.2%) | 147 (+8.9%) |
| Average Probe | 0.50 | 13 (+769%) | 1.49 | 28 (+275%) |
4.46 | 67 (+34.9%) |
| Max Probe | 12 (-72.1%) | 13 (-74.0%) | 24 (-86.7%) | 28 (-88.5%) |
58 (-96.4%) | 67 (-95.2%) |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
Maximum probe lengths improve dramatically, undercutting even quadratic probing and double hashing. This solves the main problem with open addressing.
However, performance gains are less clear-cut:
Fortunately, we’ve got one more trick up our sleeves.
When erasing a key, we can run a very similar backshift deletion algorithm. There are just two differences:
With backshift deletion, we no longer need to keep track of the maximum probe length.
Implementing this table, compared to naive robin hood probing:
| Robin Hood + Backshift | 50% Load | 75% Load | 90% Load | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 52 | 78 | 118 | |||
| Erase (ns/key) | 31 (+63.0%) | 47 (+52.7%) | 59 (-23.3%) | |||
| Lookup (ns/key) | 19 | 33 (-43.3%) | 31 | 74 (-32.2%) | 80 | 108 (-26.1%) |
| Average Probe | 0.50 | 0.75 (-94.2%) | 1.49 | 1.87 (-93.3%) | 4.46 | 4.95 (-92.6%) |
| Max Probe | 12 | 12 (-7.7%) | 24 | 25 (-10.7%) | 58 | 67 |
| Memory Amplification | 2.00 | 1.33 | 1.11 | |||
We again regress the performance of erase, but we finally achieve reasonable missing-key behavior. Given the excellent maximum probe lengths and overall query performance, Robin Hood probing with backshift deletion should be your default choice of hash table.
You might notice that at 90% load, lookups are significantly slower than basic linear probing. This gap actually isn’t concerning, and explaining why is an interesting exercise.7
Our Robin Hood table has excellent query performance, and exhibited a maximum probe length of only 12—it’s a good default choice. However, another class of hash tables based on Cuckoo Hashing can provably never probe more than a constant number of buckets. Here, we will examine a particularly practical formulation known as Two-Way Chaining.
Our table will still consist of a flat array of buckets, but each bucket will be able to hold a small handful of keys. When inserting an element, we will hash the key with two different functions, then place it into whichever corresponding bucket has more space. If both buckets happen to be filled, the entire table will grow and the insertion is retried.
You might think this is crazy—in separate chaining, the expected maximum probe length scales with \(O(\frac{\lg N}{\lg \lg N})\), so wouldn’t this waste copious amounts of memory growing the table? It turns out adding a second hash function reduces the expected maximum to \(O(\lg\lg N)\), for reasons explored elsewhere. That makes it practical to cap the maximum bucket size at a relatively small number.
Let’s implement a flat two-way chained table. As with double hashing, we can use the high bits of our hash to represent the second hash function.
| Two-Way Chaining | Capacity 2 | Capacity 4 | Capacity 8 | |||
| Existing | Missing | Existing | Missing | Existing | Missing | |
| Insert (ns/key) | 265 | 108 | 111 | |||
| Erase (ns/key) | 24 | 34 | 45 | |||
| Lookup (ns/key) | 23 | 23 | 30 | 30 | 39 | 42 |
| Average Probe | 0.03 | 0.24 | 0.74 | 2.73 | 3.61 | 8.96 |
| Max Probe | 3 | 4 | 6 | 8 | 13 | 14 |
| Memory Amplification | 32.00 | 4.00 | 2.00 | |||
Since every key can be found in one of two possible buckets, query times become essentially deterministic. Lookup times are especially impressive, only slightly lagging the Robin Hood table and having no penalty on missing keys. The average probe lengths are very low, and max probe lengths are strictly bounded by two times the bucket size.
The table size balloons when each bucket can only hold two keys, and insertion is very slow due to growing the table. However, capacities of 4-8 are reasonable choices for memory unconstrained use cases.
Overall, two-way chaining is another good choice of hash table, at least when memory efficiency is not the highest priority. In the next section, we’ll also see how lookups can even further accelerated with prefetching and SIMD operations.
Remember that deterministic queries might not matter if you haven’t already implemented incremental table growth.
Cuckoo hashing involves storing keys in two separate tables, each of which holds one key per bucket. This scheme will guarantee that every key is stored in its ideal bucket in one of the two tables.
Each key is hashed with two different functions and inserted using the following procedure:
If the loop ends up evicting the key we’re trying to insert, we know it has found a cycle and hence must grow the table.
Because Cuckoo hashing does not strictly bound the insertion sequence length, I didn’t benchmark it here, but it’s still an interesting option.
So far, the lookup benchmark has been implemented roughly like this:
for(uint64_t i = 0; i < N; i++) {
assert(table.find(keys[i]) == values[i]);
}
Naively, this loop runs one lookup at a time. However, you might have noticed that we’ve been able to find keys faster than the CPU can load data from main memory—so something more complex must be going on.
In reality, modern out-of-order CPUs can execute several iterations in parallel. Expressing the loop as a dataflow graph lets us build a simplified mental model of how it actually runs: the CPU is able to execute a computation whenever its dependencies are available.
Here, green nodes are resolved, in-flight nodes are yellow, and white nodes have not begun:
In this example, we can see that each iteration’s root node (i++) only requires the value of i from the previous step—not the result of find.
Therefore, the CPU can run several find nodes in parallel, hiding the fact that each one takes ~100ns to fetch data from main memory.
There’s a common optimization strategy known as loop unrolling. Unrolling involves explicitly writing out the code for several semantic iterations inside each actual iteration of a loop. When each inner pseudo-iteration is independent, unrolling explicitly severs them from the loop iterator dependency chain.
Most modern x86 CPUs can keep track of ~10 simultaneous pending loads, so let’s try manually unrolling our benchmark 10 times.
The new code looks like the following, where index_of hashes the key but doesn’t do the actual lookup.
uint64_t indices[10];
for(uint64_t i = 0; i < N; i += 10) {
for(uint64_t j = 0; j < 10; j++) {
indices[j] = table.index_of(keys[i + j]);
}
for(uint64_t j = 0; j < 10; j++) {
assert(table.find_index(indices[j]) == values[i + j]);
}
}
This isn’t true unrolling, since the inner loops introduce dependencies on j.
However, it doesn’t matter in practice, as computing j is never a bottleneck.
In fact, our compiler can automatically unroll the inner loop for us (clang in particular does this).
| Lookups (ns/find) | Naive | Unrolled |
| Separate Chaining (100%) | 35 | 34 |
| Linear (75%) | 36 | 35 |
| Quadratic (75%) | 31 | 31 |
| Double (75%) | 38 | 37 |
| Robin Hood (75%) | 31 | 31 |
| Two-Way Chaining (x4) | 30 | 32 |
Explicit unrolling has basically no effect, since the CPU was already able to saturate its pending load buffer. However, manual unrolling now lets us introduce software prefetching.
When traversing memory in a predictable pattern, the CPU is able to preemptively load data for future accesses. This capability, known as hardware prefetching, is the reason our flat tables are so fast to iterate. However, hash table lookups are inherently unpredictable: the address to load is determined by a hash function. That means hardware prefetching cannot help us.
Instead, we can explicitly ask the CPU to prefetch address(es) we will load from in the near future. Doing so can’t speed up an individual lookup—we’d immediately wait for the result—but software prefetching can accelerate batches of queries. Given several keys, we can compute where each query will access the table, tell the CPU to prefetch those locations, and then start actually accessing the table.
To do so, let’s make table.index_of prefetch the location(s) examined by table.find_indexed:
Importantly, prefetching requests the entire cache line for the given address, i.e. the aligned 64-byte chunk of memory containing that address. That means surrounding data (e.g. the following keys) may also be loaded into cache.
| Lookups (ns/find) | Naive | Unrolled | Prefetched |
| Separate Chaining (100%) | 35 | 34 | 26 (-22.6%) |
| Linear (75%) | 36 | 35 | 23 (-36.3%) |
| Quadratic (75%) | 31 | 31 | 22 (-27.8%) |
| Double (75%) | 38 | 37 | 33 (-12.7%) |
| Robin Hood (75%) | 31 | 31 | 22 (-29.4%) |
| Two-Way Chaining (x4) | 30 | 32 | 19 (-40.2%) |
Prefetching makes a big difference!
Modern CPUs provide SIMD (single instruction, multiple data) instructions that process multiple values at once. These operations are useful for probing: for example, we can load a batch of \(N\) keys and compare them with our query in parallel. In the best case, a SIMD probe sequence could run \(N\) times faster than checking each key individually.
Let’s implement SIMD-accelerated lookups for linear probing and two-way chaining, with \(N=4\):
| Lookups (ns/find) | Naive | Unrolled | Prefetched | Missing |
| Linear (75%) | 36 | 35 | 23 | 88 |
| SIMD Linear (75%) | 39 (+10.9%) | 42 (+18.0%) | 27 (+19.1%) | 98 (-21.2%) |
| Two-Way Chaining (x4) | 30 | 32 | 19 | 30 |
| SIMD Two-Way Chaining (x4) | 28 (-6.6%) | 30 (-4.6%) | 17 (-9.9%) | 19 (-35.5%) |
Unfortunately, SIMD probes are slower for the linearly probed table—an average probe length of \(1.5\) meant the overhead of setting up an (unaligned) SIMD comparison wasn’t worth it. However, missing keys are found faster, since their average probe length is much higher (\(29.5\)).
On the other hand, two-way chaining consistently benefits from SIMD probing, as we can find any key using at most two (aligned) comparisons. However, given a bucket capacity of four, lookups only need to query 1.7 keys on average, so we only see a slight improvement—SIMD would be a much more impactful optimization at higher capacities. Still, missing key lookups get significantly faster, as they previously had to iterate through all keys in the bucket.
Updated 2023/04/05: additional optimizations for quadratic, double hashed, and two-way tables.
| Table | Insert |
Erase |
Find |
Unrolled |
Prefetched |
Avg Probe |
Max Probe |
Find DNE |
DNE Avg |
DNE Max |
Clear (ms) |
Iterate (ms) |
Memory |
| Chaining 50 | 115 | 110 | 28 | 26 | 21 | 1.2 | 7 | 28 | 0.5 | 7 | 113.1 | 16.2 | 2.5 |
| Chaining 100 | 113 | 128 | 35 | 34 | 26 | 1.5 | 10 | 40 | 1.0 | 9 | 118.1 | 13.9 | 2.0 |
| Chaining 200 | 120 | 171 | 50 | 50 | 37 | 2.0 | 12 | 68 | 2.0 | 13 | 122.6 | 14.3 | 1.8 |
| Chaining 500 | 152 | 306 | 102 | 109 | 77 | 3.5 | 21 | 185 | 5.0 | 21 | 153.7 | 23.0 | 1.6 |
| Linear 50 | 46 | 47 | 20 | 20 | 15 | 0.5 | 43 | 37 | 1.5 | 50 | 1.1 | 4.8 | 2.0 |
| Linear 75 | 58 | 82 | 36 | 35 | 23 | 1.5 | 181 | 88 | 7.5 | 243 | 0.7 | 2.1 | 1.3 |
| Linear 90 | 70 | 147 | 46 | 45 | 29 | 4.5 | 1604 | 135 | 49.7 | 1403 | 0.6 | 1.2 | 1.1 |
| Quadratic 50 | 47 | 23 | 20 | 20 | 16 | 0.4 | 21 | 82 | 4.8 | 49 | 1.1 | 5.1 | 2.0 |
| Quadratic 75 | 54 | 28 | 31 | 31 | 22 | 1.0 | 46 | 93 | 5.3 | 76 | 0.7 | 2.1 | 1.3 |
| Quadratic 90 | 65 | 29 | 42 | 42 | 30 | 1.9 | 108 | 163 | 18.2 | 263 | 0.6 | 1.0 | 1.1 |
| Double 50 | 70 | 31 | 29 | 28 | 23 | 0.4 | 17 | 84 | 4.4 | 61 | 1.1 | 5.6 | 2.0 |
| Double 75 | 80 | 43 | 38 | 37 | 33 | 0.8 | 44 | 93 | 4.7 | 83 | 0.8 | 2.2 | 1.3 |
| Double 90 | 88 | 47 | 49 | 49 | 42 | 1.6 | 114 | 174 | 16.2 | 250 | 0.6 | 1.0 | 1.1 |
| Robin Hood 50 | 52 | 31 | 19 | 19 | 15 | 0.5 | 12 | 33 | 0.7 | 12 | 1.1 | 4.8 | 2.0 |
| Robin Hood 75 | 78 | 47 | 31 | 31 | 22 | 1.5 | 24 | 74 | 1.9 | 25 | 0.7 | 2.1 | 1.3 |
| Robin Hood 90 | 118 | 59 | 80 | 79 | 41 | 4.5 | 58 | 108 | 5.0 | 67 | 0.6 | 1.2 | 1.1 |
| Two-way x2 | 265 | 24 | 23 | 25 | 17 | 0.0 | 3 | 23 | 0.2 | 4 | 17.9 | 19.6 | 32.0 |
| Two-way x4 | 108 | 34 | 30 | 32 | 19 | 0.7 | 6 | 30 | 2.7 | 8 | 2.2 | 3.7 | 4.0 |
| Two-way x8 | 111 | 45 | 39 | 39 | 28 | 3.6 | 13 | 42 | 9.0 | 14 | 1.1 | 1.5 | 2.0 |
| Two-way SIMD | 124 | 46 | 28 | 30 | 17 | 0.3 | 1 | 19 | 1.0 | 1 | 2.2 | 3.7 | 4.0 |
Actually, this prior shouldn’t necessarily apply to hash tables, which by definition have unpredictable access patterns. However, we will see that flat storage still provides performance benefits, especially for linear probing, whole-table iteration, and serial accesses. ↩
To account for various deletion strategies, the find-missing benchmark was run after the insertion & erasure tests, and after inserting a second set of elements.
This sequence allows separate chaining’s reported maximum probe length to be larger for missing keys than existing keys.
Looking up the latter set of elements was also benchmarked, but results are omitted here, as the tombstone-based tables were simply marginally slower across the board. ↩
AMD 5950X @ 4.4 GHz + DDR4 3600/CL16, Windows 11 Pro 22H2, MSVC 19.34.31937.
No particular effort was made to isolate the benchmarks, but they were repeatable on an otherwise idle system.
Each was run 10 times and average results are reported. ↩
Virtual memory allows separate regions of our address space to refer to the same underlying pages. If we map our table twice, one after the other, probe traversal never has to check whether it needs to wrap around to the start of the table. Instead, it can simply proceed into the second mapping—since writes to one range are automatically reflected in the other, this just works.
You might expect indexing a prime-sized table to require an expensive integer mod/div, but it actually doesn’t. Given a fixed set of possible primes, a prime-specific indexing operation can be selected at runtime based on the current size. Since each such operation is a modulo by a constant, the compiler can translate it to a fast integer multiplication. ↩
A Sattolo traversal causes each lookup to directly depend on the result of the previous one, serializing execution and preventing the CPU from hiding memory latency. Hence, finding each element took ~100ns in every type of open table: roughly equal to the latency of fetching data from RAM. Similarly, each lookup in the low-load separately chained table took ~200ns, i.e. \((1 + \text{Chain Length}) * \text{Memory Latency}\) ↩
First, any linearly probed table requires the same total number of probes to look up each element once—that’s why the average probe length never improved. Every hash collision requires moving some key one slot further from its index, i.e. adds one to the total probe count.
Second, the cost of a lookup, per probe, can decrease with the number of probes required. When traversing a long chain, the CPU can avoid cache misses by prefetching future accesses. Therefore, allocating a larger portion of the same total probe count to long chains can increase performance.
Hence, linear probing tops this particular benchmark—but it’s not the most useful metric in practice. Robin Hood probing greatly decreases maximum probe length, making query performance far more consistent even if technically slower on average. Anyway, you really don’t need a 90% load factor—just use 75% for consistently high performance. ↩
Is the CPU smart enough to automatically prefetch addresses contained within the explicitly prefetched cache line? I’m pretty sure it’s not, but that would be cool. ↩